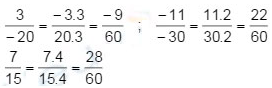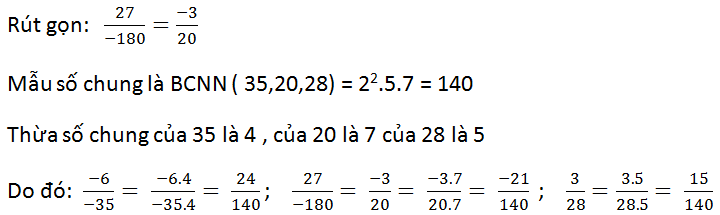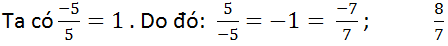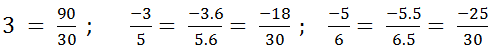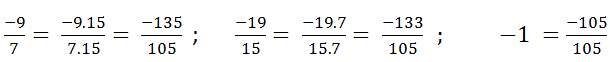Mục lục
* * * * *
a) Quy đồng mẫu các phân số sau :
\(\dfrac{-3}{16};\dfrac{5}{24};\dfrac{-21}{56}\)
b) Trong các phân số đã cho, phân số nào chưa tối giản ?
Từ nhận xét đó, ta có thể quy đồng mẫu các phân số này như thế nào ?
Hướng dẫn giải
a)
Bước 1: Tìm BCNN của 16, 24, 56 để làm MSC
16 = 24
24 = 23.3
56 = 23.7
=> BCNN(16, 24, 56) = 24.3.7 = 336
Do đó MSC của ba phân số là 336.
Bước 2: Tìm thừa số phụ của mỗi mẫu.
– Thừa số phụ của 16 là 336 : 16 = 21
– Thừa số phụ của 24 là 336 : 24 = 14
– Thừa số phụ của 56 là 336 : 56 = 6
Bước 3: Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng:
b)
Do đó: Để việc quy đồng mẫu số được đơn giản hơn ta nên rút gon phân số chưa tối giản trước khi quy đồng mẫu số.
Quy đồng mẫu các phân số sau :
a) \(\dfrac{3}{8}\) và \(\dfrac{5}{27}\)
b) \(\dfrac{-2}{9}\) và \(\dfrac{4}{25}\)
c) \(\dfrac{1}{15}\) và \(-6\)
Hướng dẫn giải
a) và
; b)
và
; c)
và
.
Quy đồng mẫu các phân số sau :
a) \(\dfrac{11}{120}\) và \(\dfrac{7}{40}\)
b) \(\dfrac{24}{146}\) và \(\dfrac{6}{13}\)
c) \(\dfrac{7}{30};\dfrac{13}{60};\dfrac{-9}{40}\)
d) \(\dfrac{17}{60};\dfrac{-5}{18};\dfrac{-64}{90}\)
Hướng dẫn giải
a)\(\dfrac{11}{120};\dfrac{21}{120}\)
b)\(\dfrac{312}{1898};\dfrac{876}{1898}\)
c)\(\dfrac{28}{120};\dfrac{26}{120};\dfrac{-27}{120}\)
d)\(\dfrac{51}{180};\dfrac{-50}{180};\dfrac{-128}{180}\)
Hai phân số sau đây có bằng nhau không ?
a) \(\dfrac{-5}{14}\) và \(\dfrac{30}{-84}\)
b) \(\dfrac{-6}{102}\) và \(\dfrac{-9}{153}\)
Hướng dẫn giải
a) Hai phân số này bằng nhau, vì:
-5.(-84)=30.14= 420 (thoả mãn tính chất nhân chéo)
b) Hai phân số này bằng nhau, vì
153.(-6)=102.(-9)=-918 (thoả mãn tính chất nhân chéo)
Quy đồng mẫu các phân số :
a) \(\dfrac{-4}{7};\dfrac{8}{9};\dfrac{-10}{21}\)
b) \(\dfrac{5}{2^2.3};\dfrac{7}{2^3.11}\)
Hướng dẫn giải
a)\(\dfrac{-36}{63};\dfrac{56}{63};\dfrac{-30}{63}\)
b)\(\dfrac{110}{264};\dfrac{21}{264}\)
Quy đồng mẫu các phân số :
a) \(\dfrac{3}{-10};\dfrac{-11}{-30};\dfrac{7}{15}\)
b) \(\dfrac{-6}{-35};\dfrac{27}{-180};\dfrac{-3}{-28}\)
Hướng dẫn giải
a) Mẫu số chung là BCNN (20, 30, 15) = 60
Thừa số phụ của 20 là 3; của 30 là 2; của 15 là 4. Do đó:
b)
Quy đồng mẫu các phân số :
a) \(\dfrac{-5}{7};\dfrac{8}{7}\)
b) \(3;\dfrac{-3}{5};\dfrac{-5}{6}\)
c) \(\dfrac{-9}{7};\dfrac{-19}{15};-1\)
Hướng dẫn giải
a)
b) Mẫu số chung là BCNN (5, 6) = 30. Do đó:
c) Mẫu số chung là BCNN (7, 15) = 105. Do đó:
Rút gọn rồi quy đồng mẫu các phân số :
a) \(\dfrac{-15}{90};\dfrac{120}{600};\dfrac{-75}{150}\)
b) \(\dfrac{54}{-90};\dfrac{-180}{288};\dfrac{60}{-135}\)
Hướng dẫn giải
a) Rút gọn:
\(\dfrac{-1}{6};\dfrac{1}{5};\dfrac{-1}{2}\)
Quy đồng:
\(\dfrac{-5}{30};\dfrac{6}{30};\dfrac{-15}{30}\)
b) Rút gọn:
\(\dfrac{-3}{5};\dfrac{-5}{8};\dfrac{-4}{9}\)
Quy đồng:
\(\dfrac{-216}{360};\dfrac{-225}{360};\dfrac{-160}{360}\)
Đố vui :
Hai bức ảnh dưới đây chụp những di tích nào ?
Cho các dãy phân số sau :
\(N:\dfrac{1}{5};\dfrac{3}{10};\dfrac{2}{5};……\)
\(M:\dfrac{2}{3};\dfrac{3}{4};\dfrac{5}{6},……..\)
\(H:\dfrac{1}{6};\dfrac{1}{4};\dfrac{1}{3};…….\)
\(Y:\dfrac{1}{20};\dfrac{1}{8};\dfrac{1}{5};……\)
\(A:\dfrac{1}{7};\dfrac{5}{14};\dfrac{4}{7};….\)
\(O:\dfrac{9}{20};\dfrac{3}{5};\dfrac{3}{4};……\)
\(I:\dfrac{1}{18};\dfrac{2}{9};\dfrac{7}{18};……\)
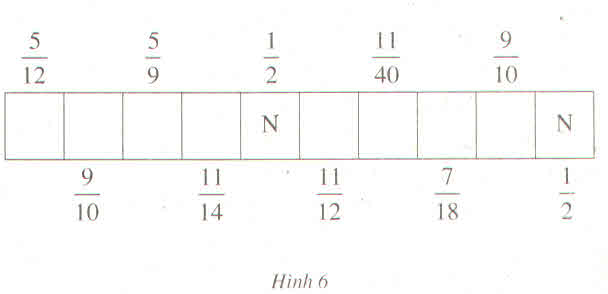
Hãy quy đồng mẫu các phân số của từng dãy rồi đoán nhận phân số thứ tư của dãy đó; viết nó dưới dạng tối giản rồi viết chữ cái ở dãy đó vào ô tương ứng với phân số ấy ở hình 6. Khi đó em sẽ biết được hai địa danh của Việt Nam được UNESCO công nhận là di sản văn hóa thế giới vào năm 1999.
Hướng dẫn giải