1. Kiến thức cần nhớ
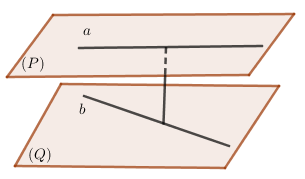
– Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung của hai đường thẳng đó.
Kí hiệu: \(d\left( {a,b} \right) = MN\) trong đó \(M \in a,N \in b\) và \(MN \bot a,MN \bot b\).
2. Phương pháp tính khoảng cách giữa hai đường thẳng
Phương pháp:
Để tính khoảng cách giữa hai đường thẳng chéo nhau ta có thể dùng một trong các cách sau:
+) Phương pháp 1: Dựng đoạn vuông góc chung $MN$ của $a$ và $b$, khi đó $d\left( {a,b} \right) = MN$.
Một số trường hợp hay gặp khi dựng đoạn vuông góc chung của hai đường thẳng chéo nhau:
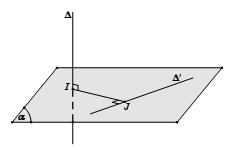
Trường hợp 1: $\Delta $ và $\Delta ‘$ vừa chéo nhau vừa vuông góc với nhau
– Bước 1: Chọn mặt phẳng $(\alpha )$ chứa $\Delta ‘$ và vuông góc với $\Delta $ tại $I$.
– Bước 2: Trong mặt phẳng $(\alpha )$ kẻ $IJ \bot \Delta ‘$.
Khi đó $IJ$ là đoạn vuông góc chung và $d(\Delta ,\Delta ‘) = IJ$.
Trường hợp 2: $\Delta $ và $\Delta ‘$ chéo nhau mà không vuông góc với nhau
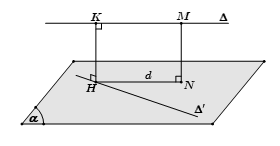
– Bước 1: Chọn mặt phẳng $(\alpha )$ chứa $\Delta ‘$ và song song với $\Delta $.
– Bước 2: Dựng $d$ là hình chiếu vuông góc của $\Delta $ xuống $(\alpha )$ bằng cách lấy điểm $M \in \Delta $ dựng đoạn $MN \bot \left( \alpha \right)$, lúc đó $d$ là đường thẳng đi qua $N$ và song song với $\Delta $.
– Bước 3: Gọi $H = d \cap \Delta ‘$, dựng $HK//MN$
Khi đó $HK$ là đoạn vuông góc chung và $d(\Delta ,\Delta ‘) = HK = MN$.
Hoặc
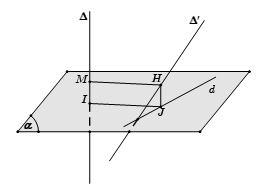
– Bước 1: Chọn mặt phẳng $(\alpha ) \bot \Delta $ tại $I$.
– Bước 2: Tìm hình chiếu $d$ của $\Delta ‘$ xuống mặt phẳng $(\alpha )$.
– Bước 3: Trong mặt phẳng $(\alpha )$, dựng $IJ \bot d$, từ $J$ dựng đường thẳng song song với $\Delta $ cắt $\Delta ‘$ tại $H$, từ $H$ dựng $HM//IJ$.
Khi đó $HM$ là đoạn vuông góc chung và $d(\Delta ,\Delta ‘) = HM = IJ$.
+) Phương pháp 2: Chọn mặt phẳng $(\alpha )$ chứa đường thẳng $\Delta $ và song song với $\Delta ‘$. Khi đó $d(\Delta ,\Delta ‘) = d(\Delta ‘,(\alpha ))$
+) Phương pháp 3: Dựng hai mặt phẳng song song và lần lượt chứa hai đường thẳng. Khoảng cách giữa hai mặt phẳng đó là khoảng cách cần tìm.
+) Phương pháp 4: Sử dụng phương pháp vec tơ
a) $MN$ là đoạn vuông góc chung của $AB$ và $CD$ khi và chỉ khi $\left\{ \begin{array}{l}\overrightarrow {AM} = x\overrightarrow {AB} \\\overrightarrow {CN} = y\overrightarrow {CD} \\\overrightarrow {MN} .\overrightarrow {AB} = 0\\\overrightarrow {MN} .\overrightarrow {CD} = 0\end{array} \right.$
b) Nếu trong $\left( \alpha \right)$ có hai vec tơ không cùng phương $\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} $ thì $OH = d\left( {O,\left( \alpha \right)} \right) \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {OH} \bot \overrightarrow {{u_1}} \\\overrightarrow {OH} \bot \overrightarrow {{u_2}} \\H \in \left( \alpha \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {OH} .\overrightarrow {{u_1}} = 0\\\overrightarrow {OH} .\overrightarrow {{u_2}} = 0\\H \in \left( \alpha \right)\end{array} \right.$