I. KIẾN THỨC CẦN NHỚ
– Cách tính chu vi của hình tam giác và chu vi hình tứ giác.
II. CÁC DẠNG TOÁN
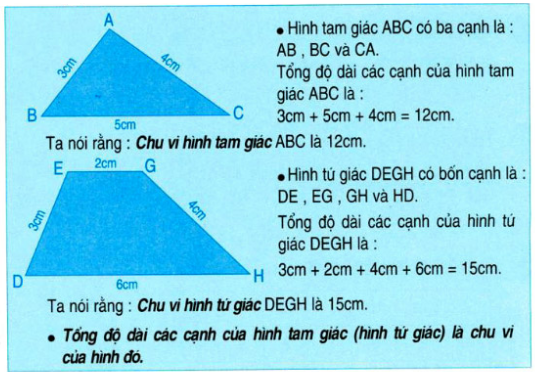
Dạng 1: Tìm chu vi của một hình tam giác.
Muốn tính chu vi của hình tam giác ta tìm tổng độ dài ba cạnh của tam giác đó.
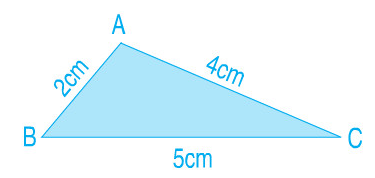
Ví dụ: Tính chu vi tam giác ABC sau:
Chu vi tam giác ABC là:
\(2 + 4 + 5 = 11\left( {cm} \right)\)
Đáp số: \(11cm\).
Dạng 2: Tìm chu vi hình tứ giác
Muốn tìm chu vi của hình tứ giác ta tìm tổng độ dài các cạnh của tứ giác.
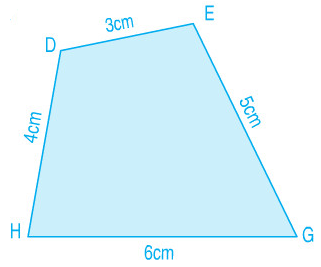
Ví dụ: Tìm chu vi của hình tứ giác sau:
Chu vi tứ giác DEGH là:
\(3 + 5 + 6 + 4 = 18\left( {cm} \right)\)
Đáp số: \(18cm\).
Dạng 3: So sánh độ dài của đường gấp khúc với chu vi hình tam giác, hình tứ giác.
– Tính độ dài đường gấp khúc, chu vi của hình tam giác, tứ giác.
– Đổi các đơn vị đo về cùng một đơn vị (nếu cần) rồi so sánh.
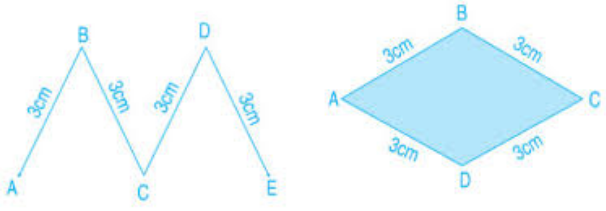
Ví dụ: So sánh độ dài đường gấp khúc ABCDE và chu vi hình tứ giác ABCD
Độ dài đường gấp khúc ABCDE là:
\(3 + 3 + 3 + 3 = 12\left( {cm} \right)\)
Chu vi hình tứ giác ABCD là:
\(3 + 3 + 3 + 3 = 12\left( {cm} \right)\)
Vậy độ dài đường gấp khúc ABCDE bằng chu vi hình tứ giác ABCD.