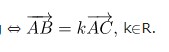Chứng minh 3 điểm thẳng hàng là một dạng toán hình thường gặp trong các kỳ thi của THCS và THPT. Bài viết hôm nay của supperclean.vn sẽ tổng hợp cách cách chứng minh 3 điểm thẳng hàng từ lớp 7 đến lớp 12. Mong rằng đây sẽ là nguồn tài liệu tham khảo hữu ích giúp các bạn làm tốt bài thi môn Toán!
3 điểm thẳng hàng khi nào?
Ba điểm được coi là thẳng hàng nhau khi chúng phân biệt và cùng thuộc 1 đường thẳng. Chỉ có 1 điểm duy nhất nằm giữa 2 điểm còn lại trong 3 điểm thẳng hàng nhau.
Như vậy, điều kiện cần và đủ đủ 3 điểm A, B, C thẳng hàng là:
-
A # B # C
-
A, B, C cùng thuộc một đường thẳng d nào đó.
Bài viết tham khảo: Tổng hợp các công thức, cách tính chu vi hình tròn
Các cách chứng minh 3 điểm thẳng hàng thông dụng nhất
Cách chứng minh số 1
Cơ sở: Chứng minh 2 góc kề có số đo bằng 180 độ (2 góc kề bù).
Ba điểm A, B, C thẳng hàng thì: ∠DBA + ∠DBC = 180°
Cách chứng minh số 2
Cơ sở: Sử dụng tiên đề ơ – clit. Đây là cách chứng minh 3 điểm thẳng hàng lớp 7 được sử dụng khá phổ biến. Theo tiên đề Ơ – Clip về 2 đường thẳng song song, qua một điểm M ở ngoài đường thẳng, chỉ có duy nhất 1 đường thẳng đi qua M và song song với đường thẳng đó.
Cách chứng: Cho đường thẳng d và điểm M nằm ngoài đường thẳng. Ta chứng minh được:
-
MA đi qua M và MA // d
-
MB đi qua M và MB // d
=> MA và MB trùng nhau, tức là 3 điểm M, B, A cùng thuộc 1 đường thẳng.
Cách chứng minh số 3
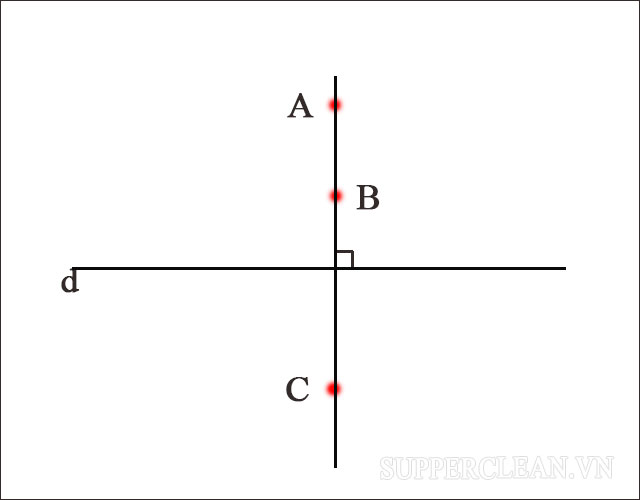
Cơ sở chứng minh: Có một và duy nhất chỉ 1 đường thẳng a’ đi qua điểm O và vuông góc với đường thẳng cho trước.
Áp dụng cơ sở trên, ta có cách chứng minh ba điểm thẳng hàng như sau:
-
AB đi qua điểm B và AB ⊥ a
-
BC đi qua điểm B và BC ⊥ a
=> Thỏa mãn 2 điều kiện trên thì AB và BC trùng nhau. Tức là 3 điểm A, B và C thẳng hàng nhau.
Cách chứng minh số 4
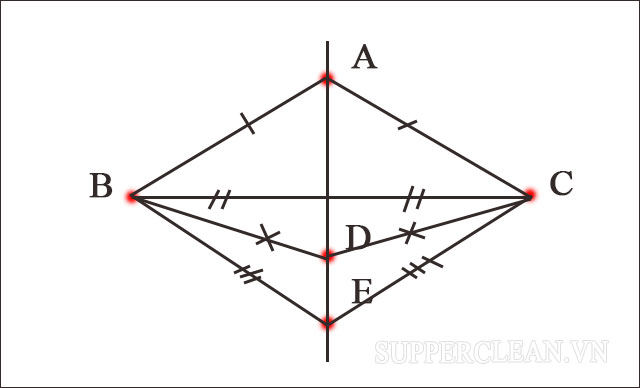
Cơ sở: Dựa vào tính chất của đường trung trực
Cho đoạn thẳng BC và các điểm A, B, E nằm ngoài đường thẳng. Nếu ta chứng minh được:
-
AB = AC => A thuộc đường trung trực của BC
-
DB = DC => D thuộc đường trung trực của BC
-
EB = EC => E thuộc đường trung trực của BC
Như vậy, A, D, và E cùng thuộc đường trung trực của BC
=> A, D và E thẳng hàng nhau.
Cách chứng minh số 5
Cơ sở: Áp dụng tính chất của đường phân giác
Cho ∠xOy và các điểm E, D, Q nằm trong góc đó. Từ các điểm E, D và Q, ta lần lượt hạ các đường vuông góc EH, EF, DI, DK, QM, QN (như dưới hình minh họa) xuống các tia Ox và Oy của góc xOy. Nếu ta chứng minh được các điều kiện sau:
-
EH = EF => E thuộc đường phân giác của góc xOy
-
DI = DK => D thuộc đường phân giác của góc xOy
-
QM = QN => Q thuộc đường phân giác của góc xOy
Thì 3 điểm E, Q, D cùng thuộc đường phân giác của góc xOy
=> Ba điểm E, Q, D thẳng hàng nhau.
Cách chứng minh số 6
Cơ sở: Trong một tam giác, có 2 đường phân giác/ đường cao/ trung tuyến cùng xuất pháp từ 1 đỉnh trùng nhau => các điểm thuộc đường phân giác/ đường cao/ trung tuyến cùng thuộc một đường thẳng.
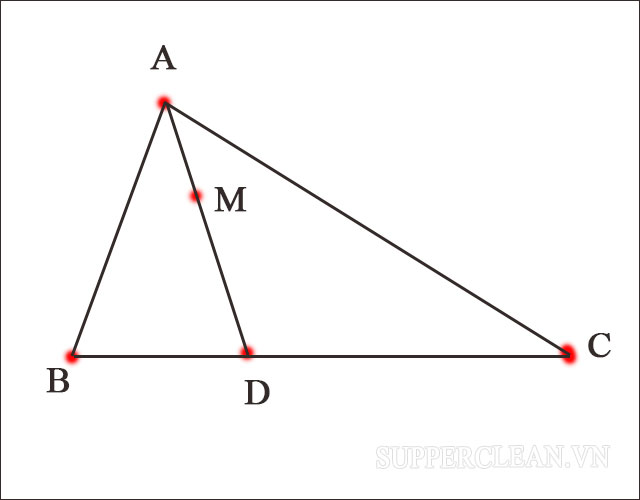
Cho tam tác BAC và 2 điểm M, D như dưới hình minh họa. Để 3 điểm A, M, D thẳng hàng nhau thì:
-
∠BAM = CAM => AM là đường phân giác của góc A
-
∠BAD = ∠ACD => AD là đường phân giác của góc A
Khi đó: AM và AD đều là đường phân giác của góc A nên hai đoạn thẳng này trùng nhau.
Tức là 3 điểm A, M và D thẳng hàng nhau.
Áp dụng cách làm tương tự với đường cao và đường trung tuyến.
Cách chứng minh số 7
Cơ sở: Sử dụng 3 đường đồng quy: Trong một tam giác, 3 đường cao hoặc 3 đường trung tuyến hoặc 3 đường phân giác sẽ cắt nhau tại 1 điểm.
Cho tam giác ABC, H là trực tâm của tam giác. Cho điểm I thuộc AB. Để 3 điểm I, H, C thẳng hàng thì ta cần phải chứng minh CI là đường cao của tam giác ABC.
=> H thuộc CI => H, C, I thẳng hàng nhau.
Áp dụng tương tự với đường phân giác và đường trung tuyến.
Cách chứng minh số 8
Cơ sở: Điều kiện 3 điểm thẳng hàng trong oxyz khi vecto AB và AC cùng phương nhau. Tức là:
=> Ba điểm A, B và C thẳng hàng.
Bài tập minh họa
Phương pháp làm: Nắm rõ các cách chứng minh 3 điểm thẳng hàng trên để áp dụng vào bài tập.
Ví dụ 1
Cho tam giác ABC, có ∠BAC = 900, M là trung điểm của đoạn thẳng AC. Kẻ tia Cx sao cho Cx vuông góc với CA (điểm B và tia Cx nằm ở 2 nửa mặt phẳng đối nhau qua bờ AC). Trên Cx lấy điểm D sao cho AB = CD. Hãy chứng minh các điểm D, M và B thẳng hàng nhau?
Lời giải:
Ví dụ 2
Tam giác ABC có điểm M và N lần lượt là trung điểm của cạnh AC và AB. Trên BM lấy điểm D và trên CN lấy điểm E sao cho M và N lần lượt là trung điểm của BD và EC. Hãy chứng minh các điểm D, A và E thẳng hàng nhau?
Lời giải:
Ví dụ 3
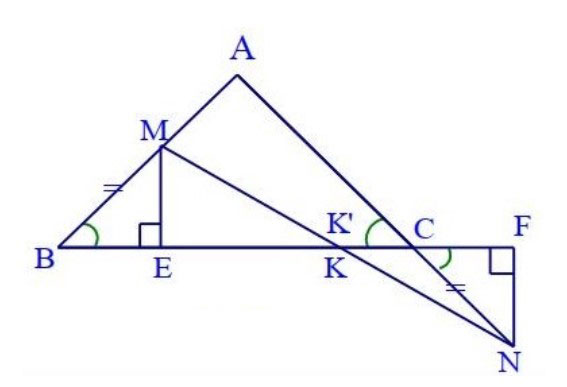
Tam giác ABC cân tại đỉnh A. Lấy điểm M thuộc cạnh AB và N thuộc cạnh AC sao cho BM = CN. Lấy điểm K là trung điểm của đoạn MN. Hãy chứng minh các điểm C, K và B thẳng hàng nhau?
Lời giải:
Ví dụ 4:
Trong tọa độ không gian Oxyz, hãy tìm trên mặt phẳng Oxz một điểm M cách đều các điểm A (1; 1; 1); điểm B (-1; 1; 0) và điểm C (3; 1; -1).
Lời giải:
Bài viết tham khảo: Số từ và lượng từ là gì? Cách phân biệt và bài tập ví dụ
Trên đây là một số cách chứng minh 3 điểm thẳng hàng mà mình đã tổng hợp. Ngoài những cách trên, bạn còn biết cách chứng minh nào khác không, hãy bình luận vào cuối bài viết cho mình biết nhé!
5/5 – (2 bình chọn)