- khoảng cách giữa hai mặt phẳng (p) 2x – y + 3z + 5 = 0 và (q) 2x – y + 3z + 1 = 0 bằng
- Khoảng cách giữa hai mặt phẳng song song lớp 11
- Khoảng cách giữa hai đường thẳng trong không gian
- Khoảng cách giữa 2 mặt phẳng hình học không gian
- Khoảng cách giữa 2 mặt phẳng lớp 11
ĐỊNH NGHĨA KHOẢNG CÁCH GIỮA 2 MẶT PHẲNG
Trước hết, chúng ta cần biết rằng trong không gian hai mặt phẳng có 3 vị trí tương đối. Đó là hai mặt phẳng trùng nhau, hai mặt phẳng song song và hai mặt phẳng cắt nhau. Trong hai trường hợp mặt phẳng cắt nhau và trùng nhau ta có thể coi khoảng cách giữa chúng bằng 0. Người ta cũng không hỏi khoảng cách giữa hai mặt phẳng trong trường hợp này. Vì vậy chúng ta chỉ xét khoảng cách giữa hai mặt phẳng song song mà thôi.
Định nghĩa:
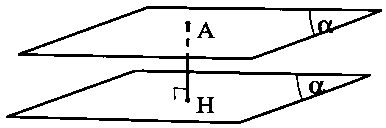
Trước hết, ta nhắc lại định nghĩa khoảng cách từ một điểm M lên mặt phẳng (P) là khoảng cách giữa M và hình chiếu của nó trên mặt phẳng (P). Ký hiệu là d(M,(P)).
Cho hai mặt phẳng (P) và (Q) song song với nhau. Khoảng cách giữa mặt phẳng (P) và (Q) là khoảng cách từ một điểm M bất kỳ trên mặt phẳng (P) đến mặt phẳng (Q) hoặc ngược lại. Ký hiệu là d((P),(Q)).
CÔNG THỨC TÍNH KHOẢNG CÁCH GIỮA HAI MẶT PHẲNG
Cho hai mặt phẳng (P), (Q) song song trong không gian. Phương trình của chúng đều có thể đưa về dạng:
(P): ax+by+cz+d=0 và (Q): ax+by+cz+d’=0 (a²+b²+c²>0 và d≠d’)
Khi đó giả sử M(α;β;γ) thuộc mặt phẳng (P) ta có: aα+bβ+cγ=-d. Khoảng cách giữa (P) và (Q) chính là khoảng cách giữa M và (Q). Do đó:
Vậy công thức tính khoảng cách giữa hai mặt phẳng song song là:
Vì vậy cách tính khoảng cách giữa hai mặt phẳng là ta biến đổi hai phương trình sao cho x, y, z có cùng hệ số sau đó mới áp dụng công thức (dòng màu xanh) bên trên.
VÍ DỤ TÍNH KHOẢNG CÁCH GIỮA 2 MẶT PHẲNG
Ví dụ:
Tính khoảng cách giữa hai mặt phẳng (P):x+2y+2z+3=0 và (Q): 2x+4y+4z-11=0.
Lời giải:
Ta còn chẳng cần phải tìm hình chiếu. Thật dễ dàng phải không nào :)) . Chúc các em thành công!
Bài tập có lời giải chi tiết
Bài tập 1. Trong không gian Oxyz, có hai mặt phẳng có phương trình lần lượt là (α): x – 2y + z + 1 = 0 và (β): x – 2y + z + 3 = 0. Hãy tính khoảng cách giữa 2 mặt phẳng?
Hướng dẫn giải
Ta thấy hai mặt phẳng này song song với nhau nên khoảng cách giữa 2 mặt phẳng được xác định theo công thức
d((α); (β)) = |1–3|12+(–2)2√+12=6√3
Xem thêm:
Công thức tính góc giữa 2 mặt phẳng
Kết luận: d((α); (β)) = 6√3
Bài tập 2. Hai mặt phẳng (α) // (β), cách nhau 3. Biết phương trình của mỗi mặt phẳng là (α): 2x – 5y – 3z + 1 = 0 và (β): ax + by + cz + d2 = 0. Hãy xác định các hệ số của phương trình mặt phẳng (β).
Hướng dẫn giải
Vì (α) // (β) => a = 2; b = – 5 và c = – 3
Mặt khác: d((α); (β)) = 3 => |1–d1|22+(–5)2+(–3)2√=3⇔d1=338−−√–1
Kết luận: Phương trình mặt phẳng (β): 2x – 5y – 3z + (338−−√–1) = 0
Ví dụ
Trong không gian Oxyz, khoảng cách giữa hai mặt phẳng (( P ): , ,x + 2y + 2z – 10 = 0 ) và (( Q ): , ,x + 2y + 2z – 3 = 0 ) bằng:
Phương pháp giải
+) Xác định được vị trí tương đối của hai mặt phẳng (P) và (Q).
+) Hai mặt phẳng (P) và (Q) song song với nhau thì: d((P),(Q))=d(M,(Q))d((P),(Q))=d(M,(Q)) với MM là một điểm thuộc (P).(P).
+) Sử dụng công thức tính khoảng cách từ điểm M(x;y;z)M(x0;y0;z0) đến mặt phẳng (P):ax+by+cz+d=(P):ax+by+cz+d=0 là:
d(M;(P))=|ax+by+cz+d|√a2+b2+c2.
Traloitructuyen.com cũng giúp giải đáp những vấn đề sau đây:
- cách tính khoảng cách giữa hai mặt phẳng (p) và (q)
- Công thức tính khoảng cách giữa hai đường thẳng
- Khoảng cách giữa hai mặt phẳng lớp 11
- Tính khoảng cách giữa 2 mặt phẳng chéo nhau
- khoảng cách giữa hai mặt phẳng (p) 2x – y + 3z + 5 = 0 và (q) 2x – y + 3z + 1 = 0 bằng
- Khoảng cách giữa hai mặt phẳng song song lớp 11
- Khoảng cách giữa 2 mặt phẳng hình học không gian
- Khoảng cách giữa 2 mặt phẳng vuông góc