5/5 – (1 bình chọn)
Hình thang là một trong những loại hình học phổ biến nhất. Tuy nhiên, số người hiểu rõ hình thang là gì cũng như công thức tính diện tích hình thang ra sao lại không nhiều. Thấu hiểu được vấn đề này, trong bài viết sau, chúng tôi sẽ chia sẻ đến độc giả một số thông tin liên quan. Cùng tham khảo nhé!
Hình thang là gì?
Hình thang trong cuộc sống hiện nay chính là một trong những loại hình học phổ biến nhất. Vậy hình thang là gì? Theo toán học, hình thang được định nghĩa như sau: “Hình thang là một hình tứ giác, có 2 cạnh bên và 2 cạnh đáy, trong đó 2 cạnh đáy nằm song song với nhau”.
Hình thang trong cuộc sống hiện nay chính là một trong những loại hình học phổ biến nhất
3 loại hình thang phổ biến nhất là:
- Hình thang thường: Đây chính là hình tứ giác có tổng số đo của 4 góc bằng 360 độ, đồng thời có 2 cạnh đáy song song với nhau.
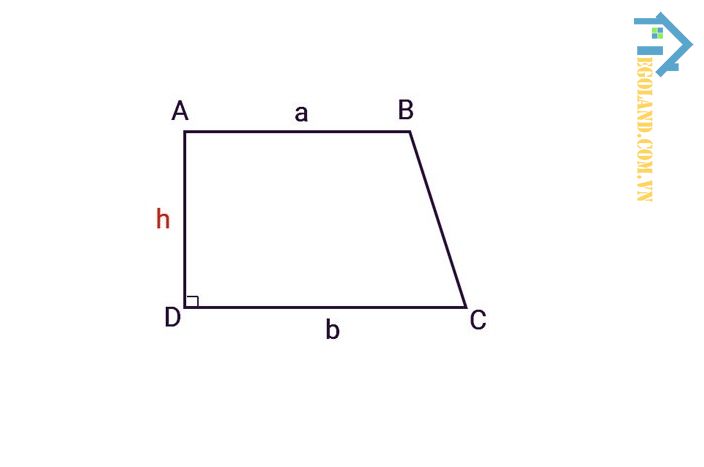
- Hình thang vuông: Đây là hình thang có chứa 1 góc bằng 90 độ.
- Hình thang cân: Đây là hình thang mà hai cạnh bên có độ dài bằng nhau và 2 góc kề một đáy bằng nhau.
Một số dạng đặc biệt của hình thang:
- Hình thoi: Đây là một loại hình thang mà 4 cạnh có độ dài bằng nhau.
- Hình bình hành: Đây là một loại hình thang có 2 cạnh bên, 2 cạnh đáy dài bằng nhau và nằm song song với nhau.
- Hình chữ nhật: Đây là hình thang có 4 góc đều bằng 90 độ và 2 cạnh bên đều vuông góc với 2 cạnh đáy.
- Hình vuông: Đây là loại hình thang có 4 góc bằng 90 độ và có 4 cạnh độ dài bằng nhau.
Tham khảo thêm các công thức tính diện tích hình khác :
Tính chất cơ bản của hình thang
Để có thể tính được diện tích hình thang một cách dễ dàng thì bạn cần phải nắm rõ về những tính chất cơ bản của hình thang. Cụ thể như sau:
Tính chất về góc
Hai góc kề với một cạnh bên của hình thanh sẽ có tổng bằng 180 độ. Bên cạnh đó, hình thang cũng có tính chất của một đường trung bình là:
- Đường trung bình của hình thang chính là trung điểm hay đường thẳng nối liền hai cạnh bên.
- Nếu một đường thẳng song song với 2 cạnh bên và đi qua trung điểm của một cạnh đáy thì đường thẳng đó cũng sẽ đi qua trung điểm của cạnh còn lại và là đường trung bình của hình thang.
- Đường trung bình của hình thang sẽ song song với cạnh đáy và có độ dài bằng ½ tổng của hai cạnh đáy.
Để có thể tính được diện tích hình thang một cách dễ dàng thì bạn cần phải nắm rõ về những tính chất cơ bản của hình thang
Tính chất về cạnh
Nếu một hình thang có độ dài hai cạnh đáy bằng nhau và nằm song song với nhau thì hai cạnh bên cũng sẽ bằng nhau và song song với nhau. Trong trường hợp này, hình thang sẽ còn được gọi là hình chữ nhật. Còn nếu như hai cạnh bên của một hình thang nằm song song với nhau thì hai cạnh đáy cũng sẽ bằng nhau. Trong trường hợp hai đường chéo của hình thang có độ dài bằng nhau thì đó chính là hình thang cân.
Công thức tính chu vi hình thang
Sau đây sẽ là những công thức tính chu vi của hình thang mà bạn nên biết:
Công thức tính chu vi cho hình thang thường
Đối với hình thang bình thường thì tổng số đo 4 cạnh của hình thang sẽ là chu vi của hình thang đó.
Công thức và cách tính chu vi cho hình thang thường như sau:
P= a + b + c + d
Trong đó:
- a, c: Độ dài của hai cạnh đáy.
- P : là chu vi hình thang thường
- b, d: Độ dài của hai cạnh bên.
Công thức tính chu vi cho hình thang vuông
Đối với hình thang vuông thì chu vi của hình thang sẽ là:
Công thức tính như sau:
P= a + b + c + d
Trong đó:
- a, c: Độ dài của hai cạnh đáy.
- P : là chu vi hình thang vuông
- b, d: Độ dài của hai cạnh bên.
Đối với hình thang thì tổng số đo 4 cạnh của hình thang sẽ là chu vi của hình thang đó
Công thức tính chu vi hình thang cân
Công thức tính chu vi của hình thang cân như sau: P= (2 x a) + b + c
Trong đó:
- a: Độ dài của 1 cạnh bên.
- b, c: Độ dài của hai cạnh đáy.
Tổng hợp các công thức tính diện tích hình thang chuẩn nhất
Để biết diện tích thì chúng ta cần phải biết cách tính chu vi của hình thang đó . Sau đây sẽ là những công thức tính diện tích hình thang chuẩn nhất mà bạn bên tham khảo :
Cách tính diện tích hình thang thường
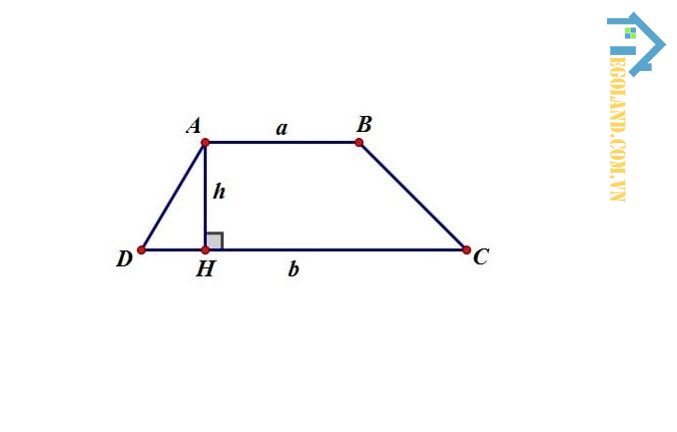
Đối với tính diện tích hình thang bình thường thì diện tích sẽ được tính bằng công thức trung bình cộng của hai cạnh đáy nhân với chiều cao của hình thang.
Công thức tính diện tích hình thang thường như sau: S = ½ h*(a + b)
Trong đó:
- S: Diện tích hình thang.
- a và b: Độ dài của 2 cạnh đáy.
- h: Độ dài cạnh bên vuông góc với 2 cạnh đáy.
Bên cạnh đó, chúng ta cũng có thể áp dụng công thức tính diện tích hình thang sau đây khi đã biết độ dài đường trung bình và chiều cao.
Công thức tính như sau:
S = độ dài chiều cao x độ dài của đường trung bình (S = h * MN)
Trong đó:
- S: Diện tích hình thang
- h: Độ dài chiều cao
- MN: Độ dài đường trung bình của hình thang
Bên cạnh đó, để có thể ghi nhớ công thức một cách dễ dàng hơn thì bạn có thể tham khảo bài thơ sau:
“Muốn tính diện tích hình thang
Đáy lớn, đáy bé ta đem cộng vào
Sau đó nhân với chiều cao
Chia đôi lấy nửa thế nào cũng ra.”
Đối với hình thang bình thường, diện tích sẽ được tính bằng công thức trung bình cộng của hai cạnh đáy nhân với chiều cao của hình thang
Cách tính diện tích hình thang cân
Tương tự như cách tích diện tích hình thang bình thường, chúng ta cũng có công thức tính diện tích hình thang cân như sau:
Công thức tính diện tích hình thang cân như sau: S = ½ h*(a + b)
Trong đó:
- S: Diện tích hình thang cân.
- h: Độ dài chiều cao của hình thang cân (độ dài đường thẳng vuông góc với đáy).
- a và b: Độ dài của 2 cạnh đáy.
Bên cạnh việc áp dụng công thức tính diện tích trên thì chúng ta cũng có thể chia hình thang cân thành những hình có diện tích nhỏ. Sau đó, tính diện tích của từng hình nhỏ rồi cộng chúng lại với nhau. Tổng kết quả sẽ chính là diện tích của hình thang cân.
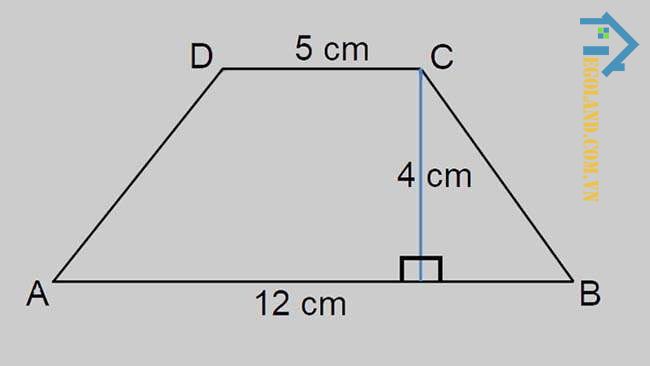
Cách tính diện tích hình thang vuông
Đối với hình thang có một góc bằng 90 độ thì độ dài của cạnh bên có góc vuông sẽ chính là độ dài của chiều cao. Bên cạnh đó, bạn cũng có thể sử dụng công thức tính diện tích hình thang bình thường để tính diện tích hình thang vuông. Tuy nhiên, chiều cao sẽ là độ dài của cạnh bên có góc 90 độ. Từ đó, chúng ta có thể dễ dàng suy ra công thức như sau:
Công thức tính hiện tích hình thang vuông như sau:
S = ½ h*(a + b)
Trong đó:
- S: Diện tích hình thang vuông
- H: Chiều cao hình thang, đối với hình thang vuông, chiều cao của hình thang bằng cạnh bên có góc vuông (AD)
- a và b: Độ dài 2 cạnh đáy song song với nhau
Đối với hình thang có một góc bằng 90 độ thì độ dài của cạnh bên có góc vuông sẽ chính là độ dài của chiều cao
Một số bài tập về hình thang
Sau đây sẽ là một số bài tập liên quan đến hình thang cũng như diện tích hình thang mà bạn có thể tham khảo:
Câu 1: Cho hình thang ABCD có độ dài đường cao là 4.2 dm, diện tích = 36.12 dm2 và đáy lớn CD dài hơn đáy bé AB là 7.8 dm. Kéo dài AD và BC cắt nhau tại E. Biết AD = ⅗ DE. Hỏi diện tích hình tam giác ABE là bao nhiêu?
Câu 2: Tính diện tích hình thang có :
- Đáy lớn 8m, đáy bé 75dm, chiều cao 32dm.
- Đáy lớn 1.9m, đáy bé 1.3m, chiều cao 0.9m.
- Đáy lớn ⅔m, đáy bé ½m, chiều cao ⅗m.
Câu 3: Tính tổng hai đáy hình thang có:
- Diện tích 3.6 dam², chiều cao 1.2 dam.
- Diện tích ¾m², chiều cao ⅔m.
- Diện tích 2400cm², chiều cao 3.8dm.
Câu 4: Tính chiều cao hình thang có:
- Diện tích 30cm², đáy lớn 8cm và đáy bé 0.4dm.
- Diện tích 6.4 dm², đáy lớn 1,8dm, đáy bé 1.4dm.
- Diện tích ¾m², đáy lớn ¼m và đáy bé ⅛m.
Câu 5: Một thửa ruộng hình thang vuông có cạnh bên vuông góc với 2 đáy dài 30.5m, đáy lớn 120.4m, đáy bé 79.6m.
- Tính diện tích thửa ruộng bằng dam²
- Trung bình 100dam2 thu được 65.2kg thóc. Hỏi trên cả thửa ruộng thu được bao nhiêu kg thóc?
Câu 6 : Một miếng đất hình thang có tổng đáy lớn, đáy bé và chiều cao là 90m. Đáy bé bằng ¾ đáy bé, chiều cao bằng ½ đáy lớn. Biết rằng cứ 2 dam² thì cần phải bón 50kg phân. Hỏi bón cả thửa ruộng thì cần phải có bao nhiêu tạ phân?
Câu 7 : Một hình thang có tổng hai đáy 110cm. Tổng của đáy lớn và chiều cao 114cm. Tổng của đáy bé và chiều cao là 68cm. Tính diện tích hình thang?
Câu 8: Một hình thang có đáy bé 2.8dm.Đáy lớn bằng 7/3 đáy bé và bằng 5/3 chiều cao. Tính diện tích hình thang.
Lời kết
Thông qua bài viết trên, chúng tôi đã chia sẻ đến bạn đọc một số thông tin liên quan đến hình thang. Hy vọng qua đó, độc giả đã có thể hiểu rõ rằng hình thang là gì cũng như công thức tính diện tích hình thang chuẩn nhất. Từ đó có thể áp dụng và tính toán một cách nhanh chóng nhất.