3.7/5 – (3 bình chọn)
Bên cạnh hình thang, hình tròn, hình tam giác,… thì hình chữ nhật cũng là một trong những loại hình học phổ biến nhất. Vậy bạn đã biết cách tính chu vi, diện tích hình chữ nhật chưa? Các công thức tính chu vi hình chữ nhật hay diện tích hình chữ nhật đã được đưa vào sách giáo khoa từ hồi cấp 1, cấp 2. Để cho học sinh có thể tiếp cận sớm với hình học không gian, phổ biến những kiến thức cơ bản nhất. Nhưng vẫn chưa có quá nhiều người nhớ được chính xác công thức tính chu vi hình chữ nhật hay diện tích hình chữ nhật là gì? Hãy cùng chúng tôi ôn lại những công thức đơn giản này nhé. Để có thêm nhiều thông tin hữu ích nhất, bạn hãy tham khảo bài viết sau của chúng tôi nhé!
Khái niệm về hình chữ nhật là gì?
Hình chữ nhật được cho là một hình học không gian có khối hình và dạng hình đơn giản nhất. Cho nên chúng đã được đưa vào bài học từ sớm để học sinh có thể làm quen với hình học từ dễ cho nên nâng cao. Hình chữ nhật tạo tiền đề cho kiến thức tính toán sau này của các em.
Đầu tiên chúng ta sẽ ôn lại kiến thức cơ bản về hình chữ nhật là gì? Vì phân biệt được hình chữ nhật thì mới có thể áp dụng đúng công thức tính diện tích hoặc chu vi hình chữ nhật một cách chính xác.
Hình chữ nhật
Hình chữ nhật trong hình học không gian là một hình tứ giác có các chiều dài giống nhau và chiều rộng cũng bằng nhau. Tính chất của hình chữ nhật và công thức tính diện tích cũng như chu vi hình chữ nhật cần được chúng ta nắm rõ một số lý thuyết dưới đây.
Tính chất cơ bản của hình chữ nhật
Tính chất của hình chữ nhật tập hợp hết tất cả những tính chất của hình thang cân và hình bình hành lại tạo nên tính chất đặc trưng cho chính nó.
Hình chữ nhật có hai cạnh luôn đối nhưng lại song song với nhau, hai canh đối đó có kích thước bằng nhau và hai góc đối cũng bằng nhau.
Tính chất đường chéo trong hình chữ nhật
Tính chất hình chữ nhật là tổng hợp vủa hình thang và hình bình hành cho nên không thể bỏ qua tính chất 2 đường chéo trong hình học không gian:
Hình chữ nhật có hai đường chéo cắt nhau ở ngay trung điểm của mỗi đường chéo, chúng có độ dài bằng nhau.
Các đường chéo trong hình chữ nhật cắt với nhau sẽ tạo nên 4 hình tam giác cân đặc biệt, từ đó hình chữ nhật được hình thành.
Từ các tính chất cơ bản của hình chữ nhật chúng ta sẽ suy ra những công thức tính diện tích hay chu vi hình chữ nhật. Xác định hai đường chéo để đi tìm công thức tính hình chữ nhật cho phù hợp nhất.
Dấu hiệu nhận biết và tính chất của hình chữ nhật
Trong hình học Euclid thì hình chữ nhật được định nghĩa là một hình tứ giác gồm có 4 góc, mỗi góc có số đo bằng 90 độ. Từ đó, chúng ta còn có thể thấy rằng hình chữ nhật còn chính là hình bình hành mà hai đường chéo có số đo bằng nhau.
Trong hình học Euclid thì hình chữ nhật được định nghĩa là một hình tứ giác gồm có 4 góc
Bên cạnh đó, HCN cũng mang những tính chất nổi bật như :
- Hai đường chéo của hình chữ nhật sẽ có độ dài bằng nhau và chúng sẽ cắt nhau tại trung điểm của mỗi đường.
- Mang đầy đủ mọi tính chất của hình thang cân và hình bình hành.
- Hai đường chéo của hình chữ nhật khi cắt nhau sẽ tạo nên bốn hình tam giác cân.
Sau đây là một số những dấu hiệu nhận biết hình chữ nhật như :
- Hình tứ giác gồm có 3 góc bằng 90 độ.
- Hình thang cân có 1 góc có số đo bằng 90 độ.
- Hình bình hành có hai đường chéo bằng nhau hoặc 1 góc vuông có số đo bằng 90 độ.
Công thức tính chu vi hình chữ nhật
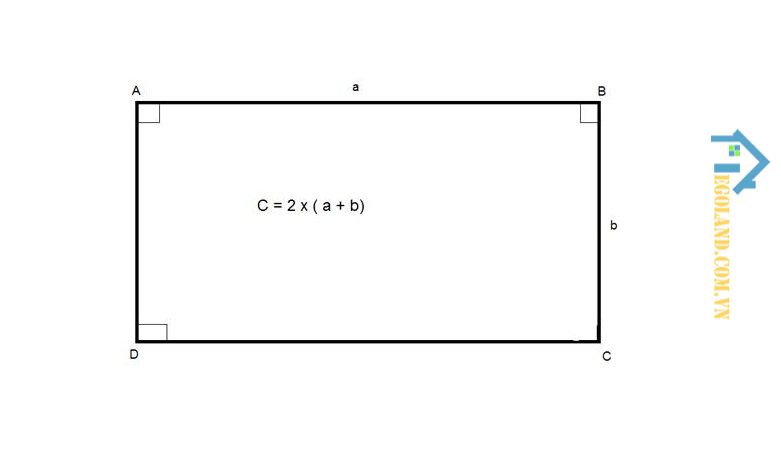
Hình chữ nhật sẽ được tính chu vi bằng tổng độ dài của những đường bao quanh hình chữ nhật. Theo đó, hình chữ nhật sẽ có chu vi bằng 2 lần của tổng chiều rộng và chiều dài.
Hình chữ nhật sẽ được tính chu vi bằng tổng độ dài của những đường bao quanh hình chữ nhật
Công thức chu vi hình chữ nhật như sau:
P = 2 x ( a + b )
Trong đó:
- P: Chu vi hình chữ nhật.
- a: Chiều dài hình chữ nhật.
- b: Chiều rộng hình chữ nhật.
Ví dụ: Một hình chữ nhật ABCD có chiều rộng bằng 3cm, chiều dài bằng 6cm. Hỏi chu vi hình chữ nhật ABCD bằng bao nhiêu?
Với bài toán đơn giản này thì chúng ta chỉ cần áp dụng công thức tính chu vi hình chữ nhật vào để giải quyết bài toán. Cụ thể như sau:
P = (a + b) x 2 = (6 + 3) x 2 = 9 × 2 = 18 cm.
Vậy, chu vi hình chữ nhật ABCD sẽ bằng 18 cm.
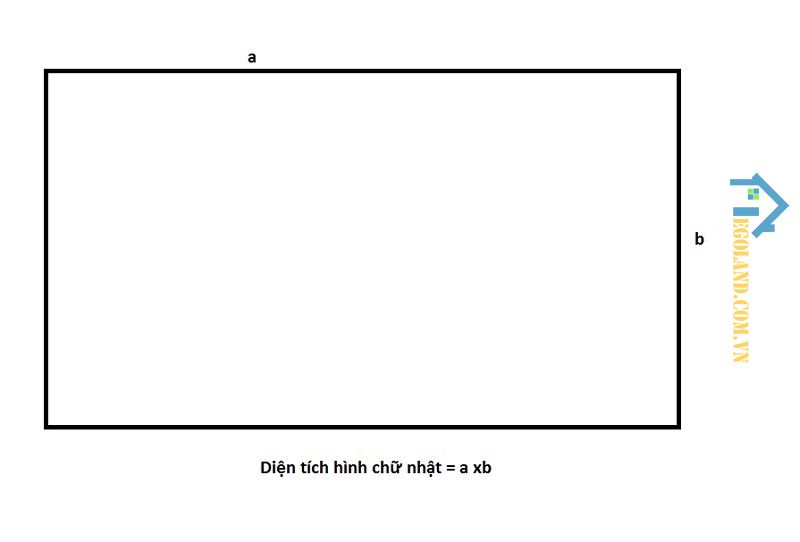
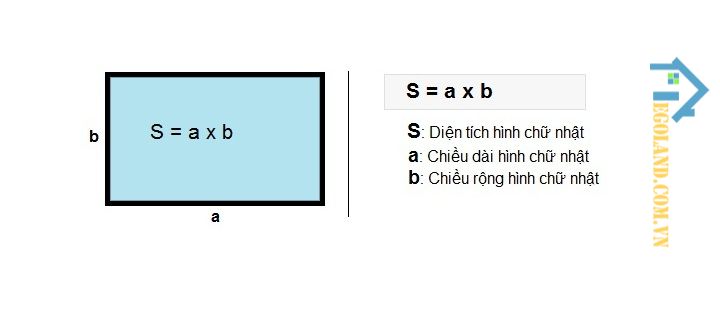
Công thức tính diện tích hình chữ nhật
Diện tích của hình chữ nhật chính là phần mặt phẳng mà chúng ta có thể nhìn thấy và được đo bằng độ lớn của bề mặt hình chữ nhật. Thế nên, diện tích của một hình chữ nhật sẽ được tính bằng chiều rộng nhân với chiều dài của hình chữ nhật đó.
Công thức như sau:
S = a x b
Trong đó:
- S: Diện tích
- a: Chiều dài
- b: Chiều rộng.
Bên cạnh đó, để có thể ghi nhớ công thức tính chu vi, diện tích của hình chữ nhật dễ dàng hơn thì bạn có thể tham khảo bài thơ sau:
“Diện tích chữ nhật tính sao
Dài nhân với rộng ra liền khó chi.
Chu vi chữ nhật cần gì
Chiều dài cộng rộng ta thì nhân hai”.
Sau đây là một số cách tính diện tích của hình chữ nhật tùy theo từng trường hợp cụ thể mà bạn nên biết:
Trường hợp 1: Tính diện tích biết cụ thể chiều rộng, chiều dài
Ví dụ: Một hình chữ nhật ABCD có chiều rộng bằng 3cm, chiều dài bằng 6cm. Hỏi diện tích của hình chữ nhật ABCD bằng bao nhiêu?
Diện tích của một hình chữ nhật sẽ được tính bằng chiều rộng nhân với chiều dài của hình chữ nhật đó
Với bài toán đơn giản này thì chúng ta chỉ cần áp dụng công thức tính diện tích của hình chữ nhật vào để giải quyết bài toán. Cụ thể như sau:
S = a x b = 6 x 3 = 18 cm2.
Vậy, diện tích của hình chữ nhật ABCD sẽ bằng 18cm2.
Trường hợp 2: Biết đường chéo và một cạnh của hình chữ nhật
Trong trường hợp này thì để có thể tính được diện tích của hình chữ nhật thì bạn cần phải tính được số đo của cạnh còn lại. Sau đó, áp dụng công thức tính diện tích để ra được kết quả.
Ví dụ: Một hình chữ nhật ABCD có đường chéo AD = c, cạnh AB = a. Tính diện tích của hình chữ nhật ABCD.
Để có thể tính được diện tích của hình chữ nhật thì điều đầu tiên bạn cần phải tính được số đo của cạnh BD bằng cách dựa vào định định lý Pytago trong tam giác vuông ABD. Sau khi đã có được kết quả số đo cạnh BD thì bạn chỉ cần lắp vào công thức tính SABCD = AB x DC.
Công thức suy rộng
Dựa vào công thức tính chu vi và diện tích hình chữ nhật ở trên, chúng ta có thể tính được chiều rộng hoặc chiều dài dựa vào số đo 1 cạnh và chu vi hoặc diện tích của hình chữ nhật đó.
Chúng ta có thể tính được chiều rộng hoặc chiều dài dựa vào số đo 1 cạnh và chu vi hoặc diện tích hình chữ nhật đó
Ví dụ: Biết số đo 1 cạnh và diện tích:
- Trong trường hợp biết chiều rộng thì chiều dài sẽ bằng diện tích chia cho chiều rộng.
- Trong trường hợp biết chiều dài thì chiều rộng sẽ bằng diện tích chia cho chiều dài.
Ví dụ: Biết số đo 1 cạnh và chu vi:
- Trong trường hợp biết chiều rộng thì chiều dài sẽ bằng chu vi chia cho 2 và trừ đi chiều rộng.
- Trong trường hợp biết chiều dài thì chiều dài sẽ bằng chu vi chia cho 2 và trừ đi chiều dài.
Một số bài toán tính diện tích, chu vi hình chữ nhật
Sau đây sẽ là một số bài toán tính diện tích hình chữ nhật được chúng tôi tổng hợp mà bạn nên tham khảo để củng cố kiến thức, rèn luyện kỹ năng cho bản thân hoặc cho con em mình:
Một số bài toán về diện tích và chu vi trong sách giáo khoa toán lớp 8
Bài 6: (SGK toán lớp 8 tập 1, trang 118)
Diện tích hình chữ nhật thay đổi như thế nào nếu:
- Chiều dài tăng 2 lần, chiều rộng không đổi?
- Chiều dài và chiều rộng tăng 3 lần?
- Chiều dài tăng 4 lần, chiều rộng giảm 4 lần ?
Bài 7: (SGK toán lớp 8 tập 1, trang 118)
Một gian phòng có nền hình chữ nhật với kích thước là 4,2m và 5,4m có một cửa sổ hình chữ nhật kích thước là 1m và 1,6m và một cửa ra vào hình chữ nhật kích thước là 1,2m và 2m.
Ta coi một gian phòng đạt mức chuẩn về ánh sáng nếu diện tích các cửa bằng 20% diện tích nền nhà. Hỏi gian phòng trên có đạt mức chuẩn về ánh sáng hay không?
Bài 15: (SGK toán lớp 8 tập 1, trang 119)
Vẽ hình chữ nhật ABCD có AB = 5cm, BC = 3cm.
- Hãy vẽ một hình chữ nhật có diện tích nhỏ hơn nhưng có chu vi lớn hơn hình chữ nhật ABCD. Vẽ được mấy hình như vậy.
- Hãy vẽ hình vuông có chu vi bằng chu vi hình chữ nhật ABCD. Vẽ được mấy hình vuông như vậy? So sánh diện tích hình chữ nhật với diện tích hình vuông có cùng chu vi vừa vẽ. Tại sao trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.
Phương thức ghi nhớ các công thức hiệu quả nhất:
Muốn ghi nhớ thật kĩ những công thức tính toán thì không thể thiếu được sự tập trung khi nghe giảng. Toán học đặc biệt là hình học không gian lúc nào cũng đem đến cảm giác khô khan cho người học cho nên cần phải tập trung kĩ để ghi nhớ.
Khi ở trên lớp cần tập trung nghe thầy cô giảng bài, kiến thức từ thầy cô lúc nào cũng bổ ích với lại nghe giảng tiếp thu tại lớp sẽ dễ ghi nhớ hơn.
Tập trung để ghi nhớ công thức tốt hơn
Nên tìm nơi yên tĩnh để học bài, tránh những nơi ồn ào dễ gây mất tập trung, ăn uống đầy đủ tăng khả năng tiếp thu.
Muốn học tốt thì nên nắm vững kiến thức của các công thức, phân biệt được tất cả các loại hình học không gian, tính chu vi hình chữ nhật, diện tích hình thoi, xác định đường chéo, trung điểm, 2 đường thẳng song song và các góc cạnh.
Áp dụng kiến thức đã học bằng cách làm thật nhiều bài tập liên quan đến diện tích và chu vi hình chữ nhật. Người ta thường bảo lý thuyết phải đi dôi với thực hành thì mới có thể giỏi lên được.
Siêng năng, cần cù chăm chỉ học tập để không bị quên kiến thức. Tất cả những kiến thức đó đều có ích cho chúng ta lúc còn đang trên ghế nhà trường hoặc thậm chí trong cuộc sống sau này.
Tổng hợp 3 bài tập về cách tính chi vi , diện tích hình chữ nhật
Bài 1: Một tấm vải hình chữ nhật có chiều dài 1m và chiều rộng là 36cm. Diện tích của tấm vải hình chữ nhật theo đơn vị xăng ti mét vuông là?
Bài giải :
Đổi 1m = 100cm
Diện tích của tấm vải hình chữ nhật là : 100 x 36 = 3600 (cm²)
Vậy diện tích hình chữ nhật sẽ là : 3600 cm²
Bài 2: Cho hình chữ nhật ABCD trong đó có chiều dài là 12 cm và chiều rộng là 5 cm. Tính diện tích và chu vi của hình chữ nhật.
Bài giải :
Áp dụng công thức tính chu vi hình chữ nhật : P = (chiều dài X chiều rộng) x 2 = (12 + 5) x 2 = 34 cm²
Áp dụng công thức tính diện tích hình chữ nhật : S = chiều dài x chiều rộng = 12 x 5 = 60 cm²
Bài 3: Cho hình chữ nhật ABCD có chiều dài 12cm và diện tích bằng 96cm². Hãy tính chiều rộng của hình chữ nhật ABCD .
Bài giải :
Dựa vào công thức tính diện tích hình chữ nhật thì ta có : S = chiều dài x chiều rộng
=> Chiều dài = S/ chiều rộng = 96/12 = 8 cm
Vậy chiều dài hình chữ nhật là : 8 cm
Một số bài toán về chu vi, diện tích tham khảo bên ngoài sách giáo khoa
Dưới đây là một số bài tập toán luyện tập giúp các bạn có thể tự tìm ra các phương pháp để tính hay áp dụng các công thức tính diện tích để giải toán .
Bài 1: Một mảnh đất hình chữ nhật có chiều dài 14 m. Nếu chiều rộng tăng 2 m, chiều dài giảm 3m thì mảnh đất đó trở thành hình vuông. Tính chu vi mảnh đất đó.
Bài 2: Một hình vuông có chu vi là 24 cm. Một hình chữ nhật có chiều rộng bằng cạnh của hình vuông và biết 3 lần cạnh hình vuông thì bằng 2 lần chiều dài hình chữ nhật. Tính diện tích mỗi hình đó.
Bài 3: Biết chu vi một hình chữ nhật gấp 6 lần chiều rộng. Hỏi chiều dài hình chữ nhật đó gấp mấy lần chiều rộng?
Bài 4: Một hình vuông được chia thành 2 hình chữ nhật. Tính chu vi hình vuông, biết rằng tổng chu vi 2 hình chữ nhật là 6420 cm.
Bài 5: Một hình chữ nhật có chu vi 72 cm. Nếu giảm chiều rộng đi 6cm và giữ nguyên chiều dài thì diện tích giảm đi 120 cm2. Tính chiều dài và chiều rộng hình chữ nhật đó.
Bài 6: Một mảnh đất hình chữ nhật có chiều dài 12 m, biết rằng 3 lần chiều rộng thì bằng 2 lần chiều dài. Tính chu vi mảnh đất đó.
Bài 7: Nếu bớt một cạnh hình vuông đi 4cm thì được hình chữ nhật có diện tích kém diện tích hình vuông 60 cm2. Tính chu vi hình vuông đó.
Bài 8: Một hình chữ nhật và một hình vuông có chu vi bằng nhau và bằng 36cm. Chiều rộng hình chữ nhật bằng 1/2 chiều dài. Hỏi diện tích hình vuông hơn diện tích hình chữ nhật bao nhiêu xăng-ti-mét vuông?
Bài 9: Một hình chữ nhật có chu vi hình chữ nhật là 64m, chiều rộng bằng 1/3 chiều dài. Tính diện tích hình chữ nhật đó.
Bài 10: Một hình chữ nhật có chiều dài gấp đôi chiều rộng. Tính chu vi hình chữ nhật đó, biết diện tích của nó là 32 cm2.
Lời kết
Trên đây là tổng hợp các công thức tính chu vi hình chữ nhật và diện tích của hình chữ nhật chuẩn nhất mà bạn nên tham khảo. Ngoài ra, chúng tôi còn giúp bạn đọc hiểu rõ hơn về cách tính chu vi cùng như dấu hiệu và tính chất của hình chữ nhật. Hy vọng qua đó bạn đã có thêm cho bản thân nhiều kiến thức hữu ích.