Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chuyên đề khoảng cách từ điểm đến mặt phẳng, tài liệu bao gồm 15 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Chuyên đề khoảng cách từ điểm đến mặt phẳng
Chuyên đề: Khoảng cách từ điểm đến mặt phẳng
I. Kiến thức cần nhớ:
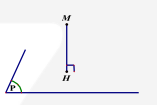
1. Khoảng cách giữa điểm và mặt phẳng
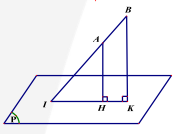
Khoảng cách giữa một điểm và một mặt phẳng là khoảng cách từ điểm đó tới hình chiếu vuông góc của nó lên mặt phẳng đó. d(M,(P)) = M H (với H là hình chiếu vuông góc của M lên mặt phẳng \((\alpha )\) ).
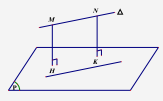
2. Khoảng cách giữa một đường thẳng và một mặt phẳng song song
Khoảng cách giữa một đường thẳng và một mặt phẳng song song là khoảng cách từ một điểm bất kì trên đường thẳng này tới mặt phẳng kia.
Nếu \(\Delta //(P)\) thì \(d(\Delta ,(P)) = d(M;(P))\) với \(\forall M \in \Delta \)
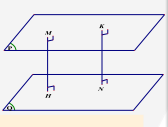
3. Khoảng cách giữa hai mặt phẳng song song
Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì trên mặt phẳng này tới mặt phẳng kia.
Nếu \((P)//(Q)\) thì d((P),(Q)) = d(M ;(Q)) = d(N ;(P)) với \(\forall M \in (P),\forall {\rm{N}} \in (Q)\)
4. Các phương pháp thường dùng để tính khoảng cách từ điểm đến mặt phẳng
a. Dùng định nghĩa
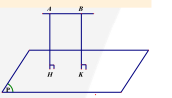
b. Phương pháp đổi điểm (dùng tỉ số khoảng cách)
* Kiến thức cần nhớ:
– Nếu đường thẳng AB song song với mặt phẳng (P) thì d(A ;(P)) =d(B ;(P))
– Nếu đường thẳng AB cắt mặt phẳng (P) tại I thì \(\frac{{d(A;(P))}}{{d(B;(P))}} = \frac{{AI}}{{BI}}\)
Chú ý: Khi sử dụng phương pháp này, ta nên cố gắng đưa việc tính
khoảng cách từ 1 điểm đến mặt phẳng về việc tính khoảng cách từ chân đường cao của hình chóp hoặc lăng trụ đến mặt phẳng.
c. Phương pháp thể tích
* \(d(M;(P)) = \frac{{3V}}{S}\) với V là thể tích của khối chóp có đỉnh là M, S là diện tích của đáy nằm trên mặt phẳng (P) của khối chóp đó
* \(d(M;(P)) = \frac{V}{S}\) với V là thể tích của khối lăng trụ có đỉnh là M, S diện tích của đáy nằm trên mặt phẳng (P) của khối lăng trụ đó .
d. Một công thức thường dùng trong bài toán tính khoảng cách
Nếu \(SI \bot (IAB)\) thì \(d(I;(SAB)) = \frac{{SI.d(I;AB)}}{{\sqrt {S{I^2} + {d^2}(I;AB)} }}\)
II. Bài tập vận dụng
1. Ví dụ minh họa
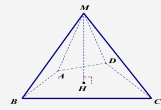
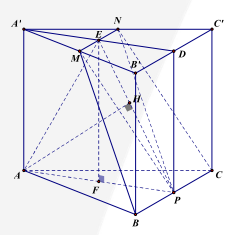
Câu 1. (Khoảng cách từ điểm đến mặt phẳng – Sử dụng phương pháp dùng định nghĩa) Cho hình lăng trụ tam giác đều \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) có \(AB = 2\sqrt 3 \) và \(A{A^\prime } = 2\). Gọi M, N, P lần lượt là trung điểm các cạnh \({A^\prime }{B^\prime },{A^\prime }{C^\prime }\) và BC. Khoảng cách từ A đến (MNP) bằng
A. \(\frac{{17}}{{65}}\)
B. \(\frac{{6\sqrt {13} }}{{65}}\)
C. \(\frac{{\sqrt {13} }}{{65}}\)
D. \(\frac{{12}}{5}\).
Lời giải
Chọn D
– Gọi \(D\) là trung điểm của \({B^\prime }{C^\prime } \Rightarrow \left\{ {\begin{array}{*{20}{l}}{MN \bot {A^\prime }D}\\{MN \bot DP}\end{array} \Rightarrow MN \bot \left( {{A^\prime }DPA} \right)} \right.\)
\( \Rightarrow (MNP) \bot \left( {{A^\prime }DPA} \right)\)
– Gọi \(E = MN \cap {A^\prime }D \Rightarrow EP\) là giao tuyến của (MNP) và \(\left( {{A^\prime }DPA} \right)\).
– Dựng \(AH \bot EP \Rightarrow AH \bot (MNP) \Rightarrow AH = d(A;(MNP))\).
– Gọi F là trung điểm của \(AP \Rightarrow EF \bot AP\) và \(EF = {A^\prime }A = 2\),
\(FP = \frac{{AP}}{2} = \frac{3}{2}\)
\( \Rightarrow EP = \sqrt {E{F^2} + F{P^2}} = \frac{5}{2} \Rightarrow AH = \frac{{EF \cdot AP}}{{EP}} = \frac{{2 \cdot 3}}{{\frac{5}{2}}} = \frac{{12}}{5}\)
Vậy \(d(A;(MNP)) = \frac{{12}}{5}\).
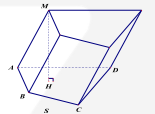
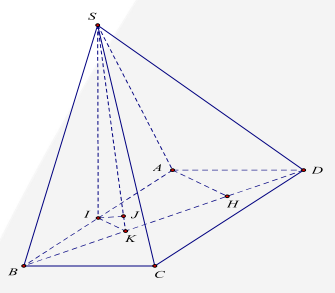
Câu 2. (Khoảng cách từ điểm đến mặt phẳng – Sử dụng phương pháp đổi điểm) Cho hình chóp S.ABCD có đáy là hình chữ nhật, cạnh AB =2AD = 2a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (ABCD) Tính khoảng cách từ điểm A đến mặt phẳng (SBD)
A. \(\frac{{a\sqrt 3 }}{4}\).
B. \( \cdot \frac{{a\sqrt 3 }}{2}\)
C. \(\frac{a}{2}\).
D. a.
Lời giải
Chọn B
Phân tích: Gọi I là trung điểm AB, ta sẽ có I là chân đường cao của hình chóp nên ta có ý tưởng đổi việc tính khoảng cách từ điểm A đến mặt phẳng (SBD) thành khoảng cách từ điểm I đến mặt phẳng (SBD).
* Kẻ \(SI \bot AB\).
Do tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (ABCD).
\( \Rightarrow I\) là trung điểm của AB và \(SI \bot (ABCD)\).
\(\Delta SAB\) đều cạnh \(2a \Rightarrow SI = \frac{{2a\sqrt 3 }}{2} = a\sqrt 3 \).
* Kẻ \({\rm{IK}} \bot {\rm{BD}}(K \in BD),{\rm{AH}} \bot {\rm{BD}}(H \in BD)\)
\( \Rightarrow IK = \frac{1}{2}AH\)
Kẻ \(IJ \bot SK,(J \in SK)(1).\)
Ta có \(\left\{ {\begin{array}{*{20}{l}}{IK \bot BD}\\{SI \bot (ABCD) \Rightarrow SI \bot BD}\end{array}} \right.\)
\( \Rightarrow BD \bot (SIK) \Rightarrow BD \bot IJ(2)\) .*
Từ (1) và (2) suy ra \(IJ \bot (SBD) \Rightarrow d(I,(SBD)) = IJ\).
Ta có:
\(\begin{array}{l}\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{D^2}}} \Rightarrow \frac{1}{{A{H^2}}} = \frac{5}{{4{a^2}}}\\ \Rightarrow AH = \frac{{2a}}{{\sqrt 5 }} \Rightarrow IK = \frac{a}{{\sqrt 5 }}\end{array}\).
\(\begin{array}{l}\frac{1}{{{\rm{I}}{{\rm{J}}^2}}} = \frac{1}{{S{I^2}}} + \frac{1}{{I{K^2}}} \Rightarrow \frac{1}{{I{J^2}}} = \frac{{16}}{{3{a^2}}}\\ \Rightarrow IJ = \frac{{a\sqrt 3 }}{4} \Rightarrow d(I,(SBD)) = \frac{{a\sqrt 3 }}{4}.\end{array}\)
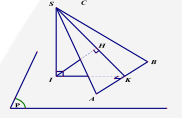
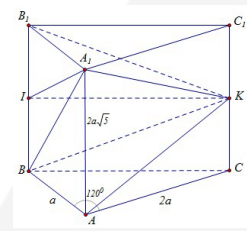
Câu 3. (Khoảng cách từ điểm đến mặt phẳng – Sử dụng phương pháp thể tích) Cho hình lăng trụ đứng \(ABC.{A_1}{B_1}{C_1}\) có \(AB = a,AC = 2a,A{A_1} = 2a\sqrt 5 \) và BAC^=120°. Gọi K, I lần lượt là trung điểm của \(C{C_1},B{B_1}\). Khoảng cách từ I đến mặt phẳng \(\left( {{A_1}BK} \right)\) bằng
A. \(a\sqrt {15} \)
\(\underline {\rm{B}} \cdot \frac{{a\sqrt 5 }}{6}\)
C. \(\frac{{a\sqrt {15} }}{3}\).
D. \(\frac{{a\sqrt 5 }}{3}\).
Lời giải
Chon B
Diện tích là:
SΔABC=12AB.AC.sinBAC^=12⋅a⋅2a⋅sin120°=a232
Thể tích khối lăng trụ \(ABC \cdot {A_1}{B_1}{C_1}\) là:
VABC⋅A1B1C1=S△ABC⋅AA1=a232⋅2a5=a315
Dễ thấy \({V_{ABC \cdot {A_1}{B_1}{C_1}}} = {V_{K \cdot {A_1}{B_1}{C_1}}} + {V_{K \cdot ABC}} + {V_{K \cdot AB{B_1}{A_1}}}\)
Mà \({V_{K \cdot {A_1}{B_1}{C_1}}} = {V_{K \cdot ABC}} = \frac{1}{6}{V_{ABC \cdot {A_1}{B_1}{C_1}}}\) nên \({V_{K \cdot AB{B_1}{A_1}}} = \frac{2}{3}{V_{ABC \cdot {A_1}{B_1}{C_1}}}\)
Ta lại có,
\(\begin{array}{l}{S_{{A_1}BI}} = \frac{1}{4} \cdot {S_{AB{B_1}{A_1}}}\\ \Rightarrow {V_{K \cdot {A_1}BI}} = \frac{1}{4} \cdot {V_{K \cdot AB{B_1}{A_1}}} = \frac{1}{4} \cdot \frac{2}{3} \cdot {V_{ABC \cdot {A_1}{B_1}{C_1}}}\\ = \frac{1}{6} \cdot {a^3}\sqrt {15} = \frac{{{a^3}\sqrt {15} }}{6}\end{array}\)
\(\begin{array}{l}BC = \sqrt {A{B^2} + A{C^2} – 2AB \cdot AC \cdot \cos A} \\ = \sqrt {{a^2} + {{(2a)}^2} – 2 \cdot a \cdot 2a \cdot \cos {{120}^0}} = a\sqrt 7 \end{array}\)
\(BK = \sqrt {B{C^2} + C{K^2}} = \sqrt {{{(a\sqrt 7 )}^2} + {{(a\sqrt 5 )}^2}} = 2a\sqrt 3 \)
\({A_1}K = \sqrt {{A_1}C_1^2 + {C_1}{K^2}} = \sqrt {{{(2a)}^2} + {{(a\sqrt 5 )}^2}} = 3a\)
\({A_1}B = \sqrt {{A_1}{A^2} + A{B^2}} = \sqrt {{{(2a\sqrt 5 )}^2} + {a^2}} = a\sqrt {21} \)
Xét thấy \(B{K^2} + {A_1}{A^2} = {A_1}{B^2} = 21{a^2}\)
Do đó, vuông tại K
\( \Rightarrow {S_{{A_1}BK}} = \frac{1}{2} \cdot {A_1}K \cdot BK = \frac{1}{2} \cdot 3{\rm{a}} \cdot 2{\rm{a}}\sqrt 3 = 3{a^2}\sqrt 3 \)
Khoảng cách từ I đến mặt phằng \(\left( {{A_1}BK} \right)\) là:
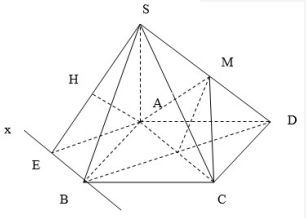
Câu 4. (Khoảng cách từ đường thẳng đến mặt phẳng song song – Sử dụng phương pháp thể tích) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và SA = 2a, M là trung điểm của SD. Tính khoảng cách d giữa đường thẳng SB và mặt phẳng (ACM).
A. \(d = \frac{{3a}}{2}\)
B. \(d = a\).
C. \(d = \frac{{2a}}{3}\).
D. \(d = \frac{a}{3}\)
Lời giải
Chọn C
Cách 1
\(d(SB,(ACM)) = d(B,(ACM))\)
=3VMABCS△ACM=34VS⋅ABCDS△ACM=34⋅2334=23
– \({V_{S.ABCD}} = \frac{1}{3} \cdot SA \cdot {S_{ABCD}} = \frac{2}{3}(a = 1)\)
– \(\begin{array}{l}AC = \sqrt 2 ,AM = \frac{1}{2}\sqrt {1 + {2^2}} = \frac{{\sqrt 5 }}{2},\\MC = \sqrt {1 + {{\left( {\frac{{\sqrt 5 }}{2}} \right)}^2}} = \frac{3}{2} \Rightarrow {S_{ACM}} = \frac{3}{4}\end{array}\)
Cách 2
Theo bài ra ta có \(SB//(ACM)\).
Qua B ta kẻ đường thẳng x song song với AC, qua A dựng \(AE \bot Bx\) thì ta có \((SBx)//(ACM)\)
Kẻ \(AH \bot SE\).
Lại có \(\left\{ {\begin{array}{*{20}{l}}{EB \bot AE}\\{EB \bot SA}\end{array} \Rightarrow EB \bot AH} \right.\)
Do đó \(AH \bot (SBx)\). Khi đó d(SB,(ACM)) = d((SBx),(ACM)) = d(A,(SBx)) = AH
\(AE = BO = \frac{{a\sqrt 2 }}{2};SA = 2a\) (O là tâm hình vuông ABCD)
\( \Rightarrow AH = \frac{{AE \cdot SA}}{{\sqrt {A{E^2} + S{A^2}} }} = \frac{{2a}}{3}{\rm{. }}\)
Vậy \(d = \frac{{2a}}{3}\)
Xem thêm