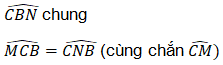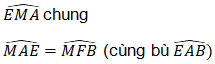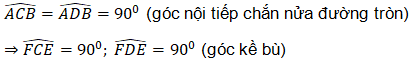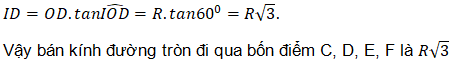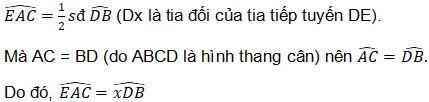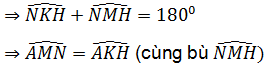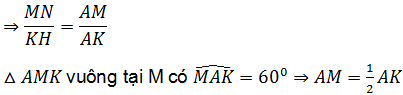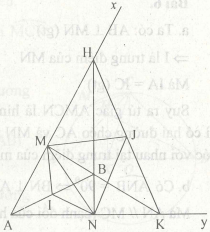Hướng dẫn học sinh lớp 9 cách chứng minh tứ giác nội tiếp bằng cách nhắc lại lý thuyết và giải các bài tập toán.
Trước tiên chúng ta cần ôn lại kiến thức về tứ giác nội tiếp (định nghĩa, dấu hiệu nhận biết tứ giác nội tiếp).
Khái niệm tứ giác nội tiếp
Tứ giác có bốn đỉnh nằm trên một đường tròn gọi là tứ giác nội tiếp (đường tròn).
Dấu hiệu nhận biết tứ giác nội tiếp
Tứ giác nội tiếp có các tính chất dưới đây:
1) Có 4 đỉnh cách đều 1 điểm nào đó. Điểm đó là tâm đường tròn ngoại tiếp tứ giác.
Cho tứ giác ABCD nội tiếp (O; R) khi đó OA = OB = OC = OD = R.
2) Có tổng 2 góc đối bằng 180°
Cho ABCD là tứ giác nội tiếp thì A+C= B+D = 1800.
3) Có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó.
Cho tứ giác nội tiếp ABCD thì: góc ngoài đỉnh A bằng góc BCD, góc ngoài đỉnh B bằng góc ADC, góc ngoài đỉnh C bằng góc BAD, góc ngoài đỉnh D bằng góc BAC.
4) 2 góc cùng nhìn 1 cạnh thì bằng nhau
Cho ABCD là tứ giác nội tiếp thì: góc DAC = góc DBC; góc DBA = góc ACD; góc CBD = góc CAD; góc BAC = góc CDB.
Các cách chứng minh tứ giác nội tiếp đường tròn
Để chứng minh một tứ giác là tứ giác nội tiếp ta cần chứng minh tứ giác đó có một trong những dấu hiệu dưới đây:
1) 4 đỉnh cách đều 1 điểm
Chứng minh cho bốn đỉnh của tứ giác cách đều một điểm nào đó
Tứ giác ABCD là tứ giác nội tiếp đường tròn tâm O ⇔ OA = OB = OC = OD
2) Có tổng 2 góc đối bằng 180°
Chứng minh tứ giác có tổng 2 góc đối bằng 180°
Tứ giác ABCD là tứ giác nội tiếp một đường tròn nếu góc A + góc C = 180° hoặc góc B + góc D = 180°
3) 2 góc nội tiếp cùng chắn 1 cung bằng nhau
Chứng minh từ hai đỉnh cùng kề một cạnh cùng nhìn một cạnh dưới hai góc bằng nhau.
Tứ giác ABCD là tứ giác nội tiếp đường tròn ⇔ góc DAC = góc DBC cùng chắn cung DC
4) Tổng 2 góc đối bằng nhau
Nếu một tứ giác có tổng số đo hai góc đối bằng nhau thì tứ giác đó nội tiếp được trong một đường tròn
Tứ giác ABCD là tứ giác nội tiếp đường tròn ⇔ góc A + góc C = góc B + góc D. Đây là trường hợp đặc biệt của cách thứ 2.
5) Góc ngoài tại đỉnh bằng góc đối của đỉnh đó
Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó thì nội tiếp được trong một đường tròn.
Tứ giác ABCD là tứ giác nội tiếp đường tròn nếu góc ngoài đỉnh A bằng góc C, hoặc góc ngoài đỉnh B bằng góc D.
6) Tứ giác là các hình đặc biệt
Chứng minh tứ giác là một trong các hình đặc biệt. Nếu tứ giác là:
– Hình vuông, hình chữ nhật, hình thang cân là tứ giác nội tiếp.
– Hình thoi, hình bình hành không là tứ giác nội tiếp.
Bài tập chứng minh tứ giác nội tiếp
Dưới đây là các bài toán về chứng minh tứ giác nội tiếp có lời giải mà Gia sư Tiến Bộ muốn chia sẻ với các em.
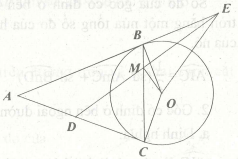
Bài 1. Cho đường tròn tâm O. Từ điểm A ở bên ngoài đường tròn (O) vẽ hai tiếp tuyến AB và AC với đường tròn (B, C là hai tiếp điểm). Trên BC lấy điểm M, vẽ đường thẳng vuông góc với OM tại M, cắt AB và AC lần lượt tại E và D. Chứng minh các tứ giác EBMO và DCOM nội tiếp được trong đường tròn. Xác định tâm các đường tròn đó.
Giải
– Chứng minh tứ giác EBMO nội tiếp
Có OM ⊥ ME (gt) nên góc OME bằng 90º
OB ⊥ BE (BE là tiếp tuyến của (O)) nên góc OBE bằng 90º
Vậy, tứ giác EBMO có hai góc vuông cùng nhìn cạnh OE nên tứ giác EBMO nội tiếp trong đường tròn đường kính OE.
– Chứng minh tứ giác DCOM nội tiếp
Có OM ⊥ OD (gt) nên góc OMD bằng 90°
CD ⊥ OC (CĐ là tiếp tuyến của (O)) nên góc OCD bằng 90°
Vậy, tứ giác DCOM có hai góc vuông cùng nhìn cạnh OD nên tứ giác DCOM nội tiếp trong đường tròn đường kính OD.
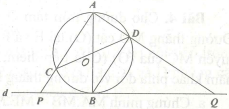
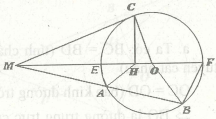
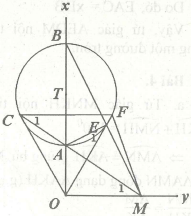
Bài 2. Cho đường tròn tâm O đường kính AB = 2R. CD là đường kính di động. Gọi d là tiếp tuyến tại B của đường tròn (O), các đường thẳng AC, AD cắt d lần lượt tại P và Q.Chứng minh tứ giác CPQD nội tiếp được đường tròn.
Giải
Ta có:
Có: góc ADB bằng 90° (góc nội tiếp chắn nửa đường tròn)
Từ (1) và (2) suy ra:
⇒ Tứ giác CPQD nội tiếp được đường tròn.
Bài 3. Qua điểm B nằm ở bên ngoài đường tròn (O), vẽ hai tiếp tuyến BC và BD với đường tròn (O), (C, D là các tiếp điểm). Từ B vẽ cát tuyến BMN (M nằm giữa B và N, tia BN nằm giữa hai tia BC và BO), gọi H là giao điểm của BO và CD.
a. Chứng minh BM.BN = BH.BO.
b. Chứng minh tứ giác OHMN nội tiếp.
Giải
a. Ta có: BC = BD (tính chất hai tiếp tuyến cắt nhau)
OC = OD (bán kính đường tròn (O))
⇒ BO là đường trung trực của CD ⇒ BO ⊥ CD (1)
△BMC và △BCN có:
Nên △BMC đồng dạng △BCN (g.g)
Do (1) ta có △BCO vuông tại C, đường cao CH:
⇒ (3)
Từ (2) và (3) ⇒ BM.BN = BH.BO.
b. Ta có: BM.BN = BH.BO (chứng minh trên)
△BMO và △BHN có:
⇒ △BMO đồng dạng △BHN (c.g.c)
⇒ Tứ giác OHMN nội tiếp (hai góc bằng nhau cùng nhìn một cạnh).
Bài 4. Cho đường tròn tâm O và điểm M nằm ngoài đường tròn (O). Đường thẳng MO cắt (O) tại E và F (ME < MF). Vẽ cát tuyến MAB và tiếp tuyến MC của (O) (C là tiếp điểm, A nằm giữa hai điểm M và B, A và C nằm khác phía đối với đường thẳng MO).
a. Chứng minh MA.MB = ME.MF.
b. Gọi H là hình chiếu vuông góc của điểm C lên đường thẳng MO. Chứng minh tứ giác AHOB nội tiếp.
Giải
a. Hai tam giác MAE và MBF có:
⇒ △MAE đồng dạng với △MBF (g.g)
Nên:
b. Do hệ thức lượng trong đường tròn ta có:
MA.MB = MC2
Mặt khác, hệ thức lượng trong tam giác vuông MCO cho ta:
MH.MO = MC2 ⇒ MA.MB = MH.MO
⇒ Tứ giác AHOB nội tiếp trong đường tròn.
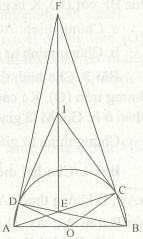
Bài 5. Cho nửa đường tròn tâm O đường kính AB = 2R. Gọi C, D là hai điểm trên nửa đường tròn đó sao cho C thuộc dây AD và góc COD bằng 120º. Gọi giao điểm của hai dây AD và BC và E, giao điểm của các đường thẳng AC và BD là F.
a. Chứng minh bốn điểm C, D, E, F cùng nẳm trên một đường tròn.
b. Tính bán kính của đường tròn đi qua C, E, D, F nói trên theo R.
a. Ta có: C, D thuộc đường tròn nên:
Giải:
Hai điểm C và D cùng nhìn đoạn thẳng FE dưới một góc bằng nhau bằng 90º nên 4 điểm C, D, E, F cùng thuộc đường tròn đường kính EF.
b. Gọi I là trung điểm EF thì ID = IC là bán kính đường tròn đi qua 4 điểm C, D, E, F nói trên.
Ta có: IC = ID ; OC = OD (bán kính đường tròn tâm O)
Suy ra IO là trung trực của CD ⇒ OI là phân giác của góc COD
Do O là trung điểm AB và tam giác ADB vuông tại D nên tam giác ODB cân tại O.
Do ID = IF nên tam giác IFD cân tại I.
Tam giác AFB có hai đường cao AD, BC cắt nhau tại E nên E là trực tâm tam giác.
⇒ FE là đường cao thứ ba.
⇒ FE vuông góc AB tại H
Từ (1), (2), (3) suy ra:
Xét tam giác vuông IDO có góc IDO bằng 60º
Ta có:
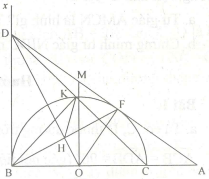
Bài 6. Cho nửa đường tròn (O) đường kính BC. Lấy điểm A trên tia đối của tia CB. Kẻ tiếp tuyến AF với nửa đường tròn (O) (F là tiếp điểm), tia AF cắt tia tiếp tuyến Bx của nửa đường tròn (O) tại D (tia tiếp tuyến Bx nằm trong nửa mặt phẳng bờ BC chứa nửa đường tròn (O)). Gọi H là giao điểm của BF với DO, K là giao điểm thứ hai của DC với nửa đường tròn (O).
a. Chứng minhh: AO.AB = AF.AD.
b. Chứng minh tứ giác KHOC nội tiếp.
Giải:
a. AF, BD là tiếp tuyến của đường tròn (O) nên AF ⊥ OF, BD ⊥ AB
Hai tam giác vuông AOF và ADB có góc OAF chung
Nên △AOF đồng dạng △ADB (g.g)
Suy ra:
b. Ta có: DB = DF (tính chất hai tiếp tuyến cắt nhau)
OB = OF (bán kính)
Nên OD là đường trung trực của BF
Suy ra: OD ⊥ BF
Lại có góc BKC bằng 90º (góc nội tiếp chắn nửa đường tròn (O)) ⇒ Tứ giác KHOC là tứ giác nội tiếp.
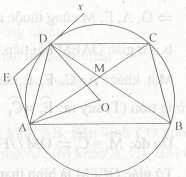
Bài 7. Cho hình thang cân ABCD (AB > CD, AB // CD) nội tiếp trong đường tròn (O). Kẻ các tiếp tuyến với đường tròn (O) tại A và D chúng cắt nhau ở E. Gọi M là giao điểm của hai đường chéo AC và BD.
Chứng minh tứ giác AEDM nội tiếp được trong một đường tròn.
Giải:
Ta có:
Vậy, tứ giác AEDM nội tiếp được trong một đường tròn.
Bài 8. Cho hai điểm A, B cố định và góc xAy bằng 60º (B thuộc miền trong góc xAy, B không thuộc Ax, Ay. Đường thẳng BN cắt Ax tại H và đường thẳng BM cắt Ay tại K. Gọi I, J lần lượt là trung điểm của AB, HK.
a. Chứng minh HK = 2MN
b. Chứng minh tứ giác MINJ nội tiếp được đường tròn.
Giải:
a. Tứ giác MNKH nội tiếp
⇒ △AMN đồng dạng △AKH (g.g)
Vậy KH = 2MN.
b. Tứ giác AMBN nội tiếp đường tròn đường kính AB.
⇒ I là tâm đường tròn ngoại tiếp tứ giác AMBN.
(góc ở tâm và góc nội tiếp cùng chắn cung MN của đường tròn ngoại tiếp tứ giác AMBN)
Tứ giác MNKH nội tiếp đường tròn tâm J đường kính HK nên:
Từ (1) và (2) có:
⇒ Tứ giác MINJ nội tiếp được trong đường tròn.
Bài 9. Cho góc vuông xOy và 2 điểm A, B trên Ox (OB > OA > 0), điểm M bất kì trên cạnh Oy (M≠O). Đường tròn (T) đường kính AB cắt tia MA, MB lần lượt tại điểm thứ hai: C, E. Tia OE cắt đường tròn (T) tại điểm thứ hai F.
a. Chứng minh bốn điểm: O, A, E, M nằm trên 1 đường tròn.
b. Tứ giác OCFM là hình gì? Tại sao?
Giải:
a.
Xét tứ giác OAEM có:
⇒ O, A, E, M cùng thuộc đường tròn.
b. Tứ giác OAEM nội tiếp, suy ra:
Mặt khác: A, C, E, F cùng thuộc đường tròn (T) suy ra:
Do đó:
Vậy tứ giác OCFM là hình thang.
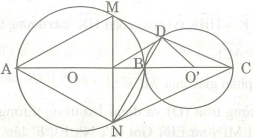
Bài 10. Cho đường tròn tâm O đường kính AB. Trên tia đối của tia AB lấy điểm C (AB>BC). Vẽ đường tròn tâm O’ đường kính BC. Gọi I là trung điểm của AC. Vẽ dây cung MN vuông góc với AC tại I, MC cắt đường tròn tâm O’ tại D.
a. Tứ giác AMCN là hình gì? Tại sao?
b. Chứng minh tứ giác NIDC nội tiếp.
Giải:
a. Ta có: AB ⊥ MN (gt)
⇒ I là trung điểm của MN
Mà IA = IC (gt)
Suy ra tứ giác AMCN là hình thoi vì có hai đường chéo AC và MN vuông góc với nhau tại trung điểm của mỗi đường.
b. Có góc ANB bằng 90º ⇒ BN ⊥ AN
Mà AN // MC (cạnh đối của hình thoi AMCN)
Suy ra BN ⊥ MC (1)
Ta lại có: góc BDC bằng 90º ⇒ BD ⊥ MC (2)
Từ (1) và (2) suy ra 3 điểm N, B, D thẳng hàng.
⇒ góc NDC bằng 90º mà góc NIC bằng 90º (vì AC ⊥ MN)
Suy ra tứ giác NIDC nội tiếp đường tròn đường kính NC.
Hình học 9 – Tags: nội tiếp, nội tiếp đường tròn, toán 9, tứ giác, tứ giác nội tiếp