Bài viết này hướng dẫn cho các em cách chứng minh 3 điểm thẳng hàng qua các ví dụ có lời giải chi tiết, dễ hiểu.
Sau mỗi ví dụ là nhận xét về hướng giải quyết một bài toán chứng minh 3 điểm thẳng hàng.
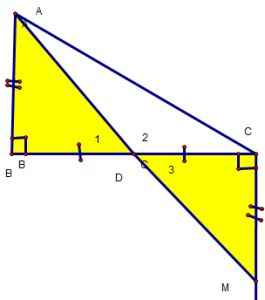
Ví dụ 1 : Cho D ABC vuông tại B. Trên nữa mặt phẳng bờ BC không có điểm A, vẽ tia Cx vuông góc BC. Trên tia Cx lấy M sao cho CM = AB. Chứng minh A, M và D là trung điểm của BC thẳng hàng.
Giải.
Xét ?ABD và ?MCD, ta có :
AB = CM (gt)
DB = DC (D là trung điểm của BC)
=> ?ABD = ?MCD (2 cạnh góc vuông)
=>
Mặt khác : (B, D, C thẳng hàng)
=>
Hay :
=> A, D, M thẳng hàng ( góc bẹt)
Nhận xét: Ở bài này chứng minh 3 điểm thẳng hàng bằng cách chứng minh cho góc tạo bởi 3 điểm đó là 180 độ.
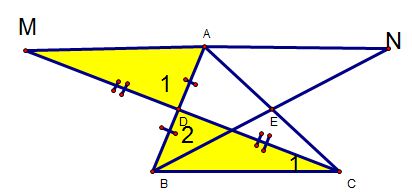
Ví dụ 2 : Cho tam giác ABC . gọi D, E lần lượt là trung điểm của AB, AC. Trên tia đối của tia DC, lấy điểm M sao cho MD = CD. Trên tia đối của tia EB, lấy điểm N sao cho EN = BE. chứng minh : A là trung điểm của MN.
GIẢI.
Xét ΔBCD và ΔBMD, ta có :
DB = DA (D là trung điểm của AB)
(đối đỉnh).
DC = DM (gt).
=> ΔBCD = ΔBMD (c -g -c)
=> và BC = AM.
Mà : ở vị trí so le trong. => BC // AM.
Chứng minh tương tự,
ta được : BC // AN và BC = AN.
ta có : BC // AM (cmt) và BC // AN (cmt)
=> A, M. N thẳng hàng. (1)
BC = AM và BC = AN => AM = AN (2).
Từ (1) và (2), suy ra : A là trung điểm của MN.
Nhận xét: Chứng minh 3 điểm A, M, N thẳng hàng trước, sau đó chứng minh AM = AN
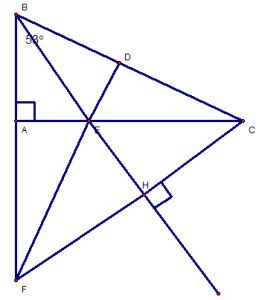
Ví dụ 3 :
Cho tam giác ABC vuông góc tại A có góc B = 530.
a) Tính góc C.
b) Trên cạnh BC, lấy điểm D sao cho BD = BA. Tia phân giác của góc B cắt cạnh AC ở điểm E. cmr : ΔBEA = ΔBED.
c) Qua C, vẽ đường thẳng vuông góc với BE tại H. CH cắt đường thẳng AB tại F. cm : ΔBHF = ΔBHC.
d) Cmr : ΔBAC = ΔBDF và D, E, F thẳng hàng.
Giải.
a. Tính góc C :
Xét ΔBAC, ta có :
=>
=>
b. ΔBEA = ΔBED :
Xét ΔBEA và ΔBED, ta có :
BE cạnh chung.
(BE là tia phân giác của góc B)
BD = BA (gt)
=> ΔBEA = ΔBED (c – g – c)
c. ΔBHF = ΔBHC
Xét ΔBHF và ΔBHC, ta có :
BH cạnh chung.
(BE là tia phân giác của góc B)
(gt)
=> ΔBHF = ΔBHC (cạnh huyền – góc nhọn)
=> BF = BC (cạnh tương ứng)
d. ΔBAC = ΔBDF và D, E, F thẳng hàng
xét ΔBAC và ΔBDF, ta có:
BC = BF (cmt)
Góc B chung.
BA = BC (gt)
=> ΔBAC = ΔBDF
=>
Mà : (gt)
Nên : hay BD
DF (1)
Mặt khác : (hai góc tương ứng của ΔBEA = ΔBED)
Mà : (gt)
Nên : hay BD
DE (2)
Từ (1) và (2), suy ra : DE trùng DF
Hay : D, E, F thẳng hàng.
Bài tập tự giải:
Ví dụ 1 : Cho tam giác ABC . Trên tia đối của tia AB lấy điểm F sao cho AB = FA. Trên tia đối của tia AC lấy điểm E sao cho AC = AE.
a) Chứng minh: Δ EAF = Δ CAB
b)Gọi K là trung điểm EF và D là trung điểm BC. Chứng minh : KB = FD.
d) Chứng minh: K, A, D thẳng hàng.
Ví dụ 2 :Cho Δ ABC có M là trung điểm của AB. Trên tia đối của tia MC lấy điểm D sao cho MD = MC.
a) Chứng minh Δ MAD = Δ MBC và AD // CB.
b) Lấy N thuộc AD; NM cắt BC tại P. Chứng minh AN = BP.
c) Trên nửa mặt phẳng bờ AB không chứa điểm D, vẽ tia AE sao cho góc EAB + góc ABC = 180^0 . Chứng tỏ D, A, E thẳng hàng.
Hình học 7 – Tags: 3 điểm thẳng hàng, thẳng hàng