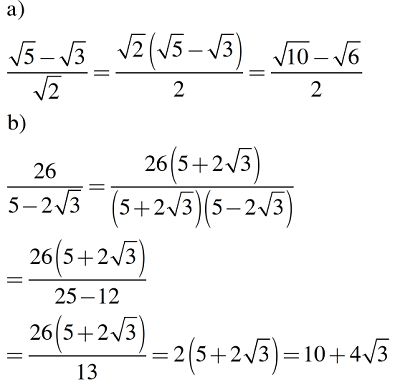Biến đổi đơn giản căn thức bậc hai và trục căn thức ở mẫu của biểu thức là dạng toán quen thuộc trong chương trình toán học lớp 9. Trong nội dung bài viết dưới đây, DINHNGHIA.VN sẽ tổng hợp kiến thức lý thuyết, bài tập ví dụ cũng như cách giải các dạng toán về chủ đề trục căn thức tại mẫu của biểu thức, cùng tìm hiểu nhé!
Cách biến đổi đơn giản căn thức bậc hai
Dưới đây là những kiến thức cần nhớ về cách biến đổi đơn giản căn thức bậc hai:
Trục căn thức tại mẫu của biểu thức
Dưới đây là lý thuyết và cách làm bài trục căn thức mẫu của phân số:
Với các biểu thức \(A,B (B>0)\), ta có;
\(A,B (B>0)\)
Với các biểu thức \(A,B,C\) \((A\geq 0, A\neq B^{2})\)
Ta có:
\(\frac{C}{\sqrt{A}+B}=\frac{C(\sqrt{A}-B)}{A-B^{2}}\)
\(\frac{C}{\sqrt{A}-B}=\frac{C(\sqrt{A}+B)}{A-B^{2}}\)
Với các biểu thức \(A,B,C\) \((A\geq 0,B\geq 0,A\neq B)\)
Ta có:
\(\frac{C}{\sqrt{A}+\sqrt{B}}=\frac{C(\sqrt{A}-\sqrt{B})}{A-B}\)
\(\frac{C}{\sqrt{A}-\sqrt{B}}=\frac{C(\sqrt{A}+\sqrt{B})}{A-B}\)
Bài tập trục căn thức ở mẫu lớp 9
Bài 50 (trang 30 SGK Toán 9 Tập 1): Trục căn thức mẫu với giả thiết các biểu thức chữ đều có nghĩa.
\(\frac{5}{\sqrt{10}}=\frac{5\sqrt{10}}{\sqrt{10}.\sqrt{10}}=\frac{5\sqrt{10}}{10}=\frac{\sqrt{10}}{2}\)
\(\frac{1}{3\sqrt{20}}=\frac{1}{3\sqrt{2^{2}.5}}=\frac{1}{3.2\sqrt{5}}=\frac{1\sqrt{5}}{6\sqrt{5}.\sqrt{5}}=\frac{\sqrt{5}}{6.5}=\frac{\sqrt{5}}{30}\)
\(\frac{2\sqrt{2}+2}{5\sqrt{2}}=\frac{(2\sqrt{2}+2)\sqrt{2}}{5\sqrt{2}.\sqrt{2}}=\frac{2(\sqrt{2})^{2}+2\sqrt{2}}{5.2}=\frac{4+2\sqrt{2}}{10}=\frac{2+\sqrt{2}}{5}\)
Bài 52 trang 30 SGK toán 9 tập 1 Trục căn thức mẫu với giả thiết các biểu thức chữ đều có nghĩa.
\(\frac{1}{\sqrt{x}-\sqrt{y}};\frac{2ab}{\sqrt{a}-\sqrt{b}}\)
-
\(\frac{1}{\sqrt{x}-\sqrt{y}}=\frac{1(\sqrt{x}+\sqrt{y})}{(\sqrt{x}-\sqrt{y})(\sqrt{x}+\sqrt{y})}=\frac{(\sqrt{x}+\sqrt{y})}{x-y}\)
(Do \(x\neq y\) nên \(\sqrt{x}\neq \sqrt{y}\)
-
\(\frac{2ab}{\sqrt{a}-\sqrt{b}}=\frac{2ab(\sqrt{a}+\sqrt{b})}{(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})}=\frac{2ab(\sqrt{a}+\sqrt{b})}{a-b}\)
(Do \(a\neq b\) nên \(\sqrt{a}\neq \sqrt{b}\).
Các bài toán trục căn thức ở mẫu khó
Ví dụ 1: Trục căn thức mẫu các biểu thức sau
-
\(\frac{\sqrt{5}-\sqrt{3}}{\sqrt{2}}\)
-
\(\frac{26}{5-2\sqrt{3}}\)
Hướng dẫn giải:
Ví dụ 2: Trục căn thức mẫu
Lý thuyết trục căn thức ở mẫu bậc 3
Công thức:
\(\frac{M}{\sqrt[3]{a}\pm \sqrt[3]{b}}=\frac{M(\sqrt[3]{a^{2}}\pm \sqrt[3]{ab}+\sqrt[3]{b^{2}})}{(\sqrt[3]{a}\pm \sqrt[3]{b})(\sqrt[3]{a^{2}}\pm \sqrt[3]{ab}+\sqrt[3]{b^{2}})}=\frac{M(\sqrt[3]{a^{2}}\pm \sqrt[3]{ab}+\sqrt[3]{b^{2}})}{a\pm b}\)
Ví dụ: Trục căn thức mẫu: \(\frac{1}{\sqrt[3]{9}-\sqrt[3]{6}+\sqrt[3]{4}}\)
Hướng dẫn giải:
Ta có: \(\frac{1}{\sqrt[3]{9}-\sqrt[3]{6}+\sqrt[3]{4}}=\frac{\sqrt[3]{3}+\sqrt[3]{2}}{(\sqrt[3]{2}+\sqrt[3]{3})(\sqrt[3]{9}-\sqrt[3]{6}+\sqrt[3]{4})}=\frac{\sqrt[3]{2}+\sqrt[3]{3}}{(\sqrt[3]{2})^{3}+(\sqrt[3]{3})^{3})}=\frac{\sqrt[3]{2}+\sqrt[3]{3}}{5}\)
Bài viết trên đây của DINHNGHIA.VN đã giúp bạn tổng hợp kiến thức cách biến đổi đơn giản căn thức bậc hai cũng như chuyên đề trục căn thức tại mẫu. Chúc bạn luôn học tập tốt!
Xem chi tiết qua bài giảng dưới đây:
(Nguồn: www.youtube.com)
Xem thêm >>> Cách xác định tâm đường tròn ngoại tiếp tam giác – Toán học lớp 9
4.1
/
5
(
30
bình chọn
)
Please follow and like us: