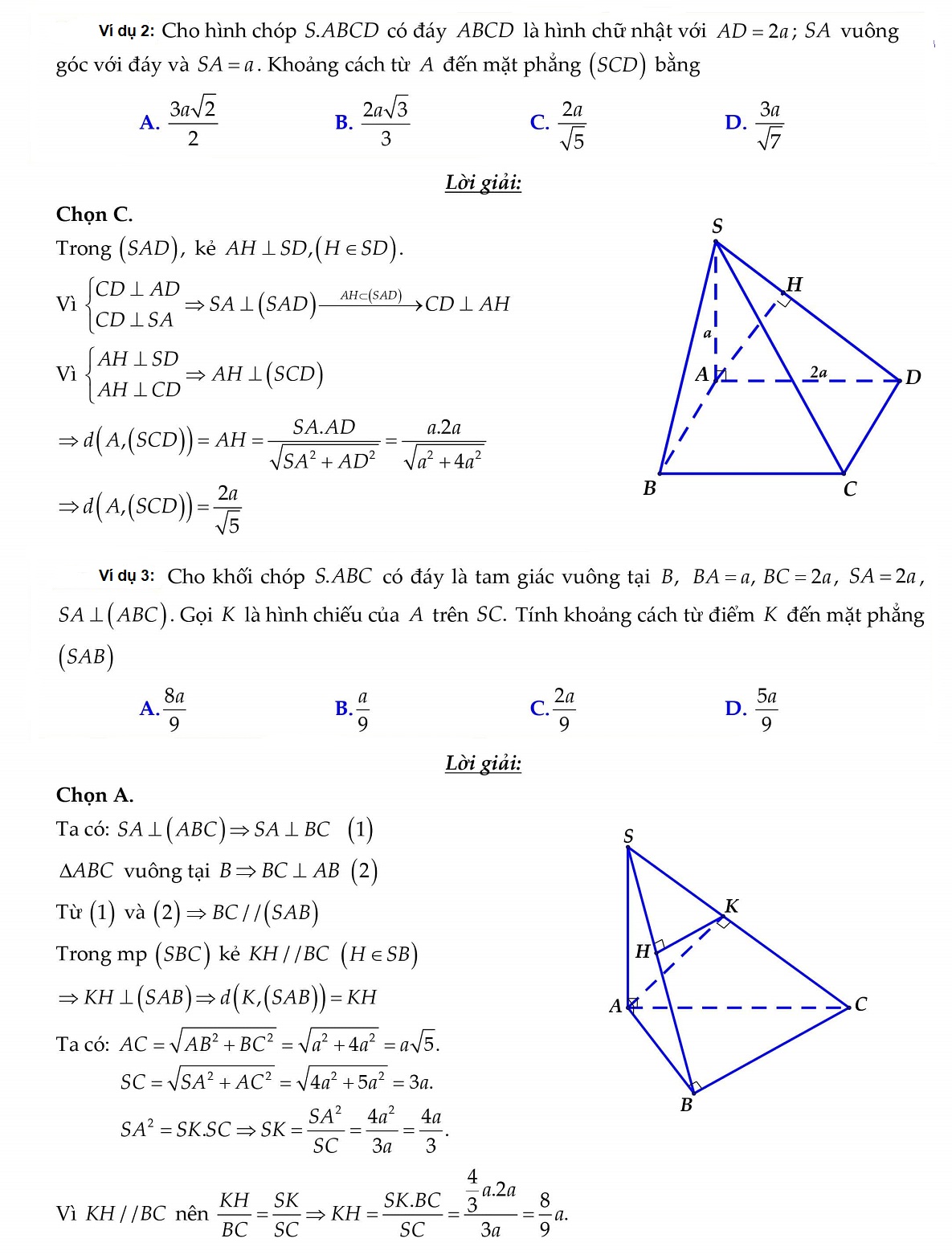
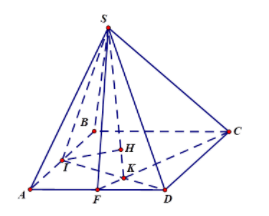
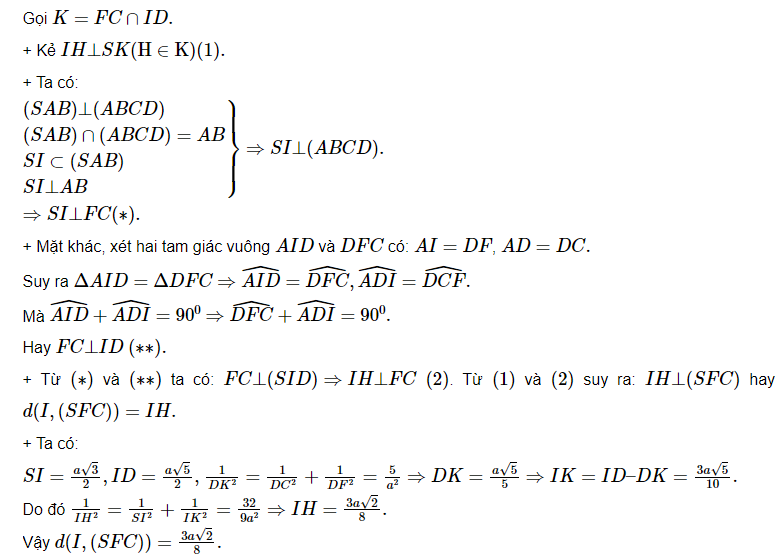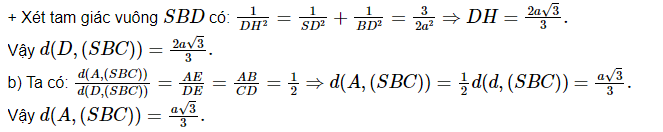Rate this post
Trong bài viết dưới đây, điện máy Sharp Việt Nam sẽ nhắc lại lý thuyết và công thức tính khoảng cách từ điểm đến mặt phẳng kèm theo các bài tập minh họa có lời giải để các bạn cùng tham khảo nhé
Khoảng cách từ điểm đến mặt phẳng là gì?
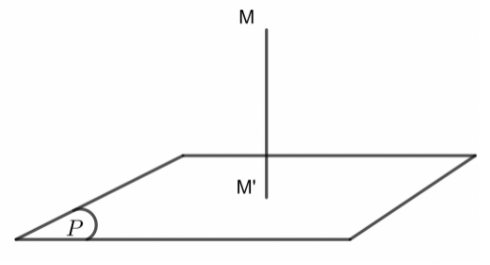
Κhοảng cách từ 1 điểm M đến mặt phẳng (P) được định nghĩa là khοảng cách từ điểm M đến hình chiếu (vuông góc) của nó trên (P). Ký hiệu là d(M,(P)).
Xem thêm: Công thức khoảng cách từ điểm đến mặt phẳng
Công thức tính khoảng cách từ điểm đến mặt phẳng
Trong không gian Oxyz, cho điểm M(α;β;γ) và mặt phẳng (P): ax + by + cz + d = 0. Khi đó, công thức khoảng cách từ 1 điểm đến mặt phẳng đã cho là:
Tham khảo thêm:
- Tích vô hướng của hai vectơ và các dạng bài tập có lời giải từ A – Z
- Cách tính góc giữa hai đường thẳng trong mặt phẳng, không gian từ A – Z
Phương pháp tìm khoảng cách từ 1 điểm đến mặt phẳng
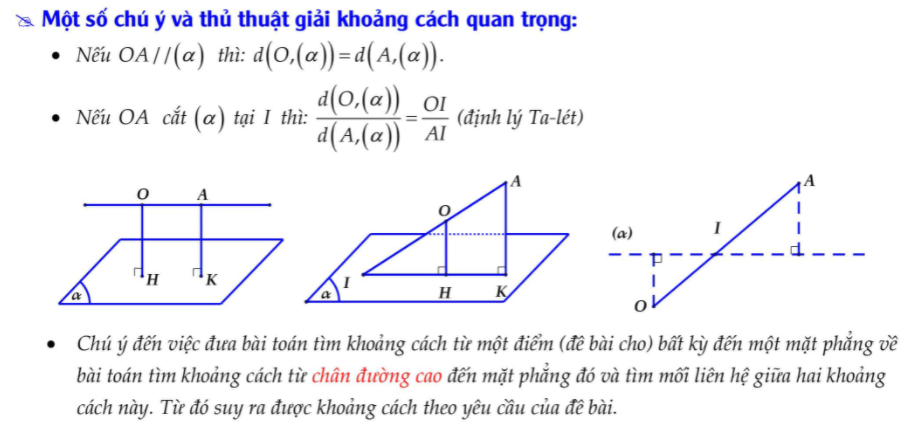
Để xác định khoảng cách từ điểm M đến mặt phẳng (P) , ta sử dụng các phương pháp sau đây:
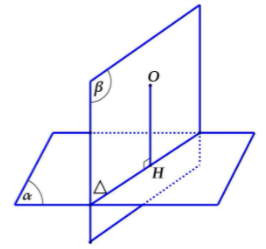
Cách 1:
Bước 1:
- Tìm hình chiếu H của O lên (α)
- Tìm mặt phẳng (β) qua O và vuông góc với (α)
- Tìm Δ = (α) ∩ (β)
- Trong mặt phẳng (β), kẻ OH ⊥ Δ tại H ⇒ H là hình chiếu vuông góc của O lên (α)
Bước 2: Khi đó OH là khoảng cách từ O đến (α)
Xem ngay: NHU CẦU VỀ DINH DƯỠNG – KHẨU PHẦN ĂN – ĐIỀU DƯỠNG- CÁC RỐI LOẠN VỀ CHỨC NĂNG TIÊU HOÁ
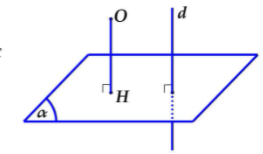
Cách 2:
Nếu đã có trước đường thẳng d ⊥ (α) thì kẻ Ox // d cắt (α) tại H. Lúc đó H là hình chiếu vuông góc của O lên (α) ⇒ d(O, (α)) = OH
Ví dụ 4: Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh a, tam giác SAB đều, (SAB) ⊥ (ABCD). Gọi I, F lần lượt là trung điểm của AB và AD. Tính d(I,(SFC))
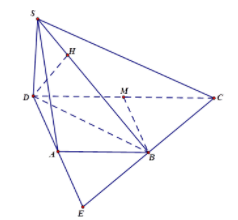
Ví dụ 5: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD = a, CD = 2a, SD ⊥ (ABCD), SD = a
a. Tính d(D,(SBC))
HOT: Tính cạnh huyền tam giác vuông và các dạng bài tập có lời giải từ A- Z
b. Tính d(A,(SBC))
Lời giải
Gọi M là trung điểm của CD, E là giao điểm của hai đường thẳng AD và BC
a. Trong mặt phẳng (SBD) kẻ DH ⊥ SB, (H ∈ SB) (1)
Vì BM = AD = ½CD => Tam giác BCD vuông tại B hay BC ⊥ BD (*). Mặt khác, vì SD ⊥ (ABCD) => SD ⊥ BC (**)
Từ (*) và (**) ta có:
BC ⊥ (SBD) => BC ⊥ DH (2)
Từ (1) và (2) suy ra: DH ⊥ (SBC) hay d(D,(SBC)) = DH
Sau khi đọc xong bài viết của chúng tôi các bạn có thể biết cách tính khoảng cách từ 1 điểm đến mặt phẳng đơn giản và chính xác nhé
HOT: Công thức ancol đơn chức