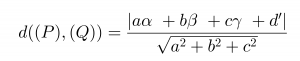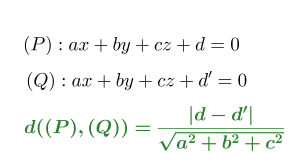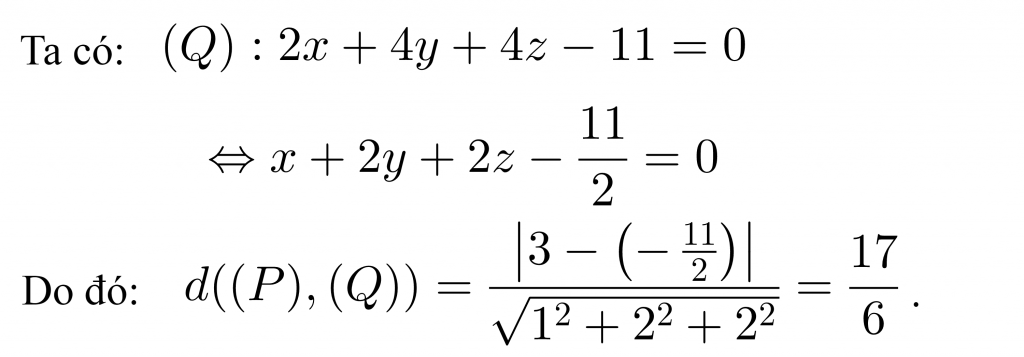Khoảng cách giữa 2 mặt phẳng trong không gian được xác định như thế nào và được tính như thế nào, công thức ra sao ?. Tất cả các vấn đề trên sẽ được giải quyết trong bài viết này.
ĐỊNH NGHĨA KHOẢNG CÁCH GIỮA 2 MẶT PHẲNG
Trước hết, chúng ta cần biết rằng trong không gian hai mặt phẳng có 3 vị trí tương đối. Đó là hai mặt phẳng trùng nhau, hai mặt phẳng song song và hai mặt phẳng cắt nhau. Trong hai trường hợp mặt phẳng cắt nhau và trùng nhau ta có thể coi khoảng cách giữa chúng bằng 0. Người ta cũng không hỏi khoảng cách giữa hai mặt phẳng trong trường hợp này. Vì vậy chúng ta chỉ xét khoảng cách giữa hai mặt phẳng song song mà thôi.
Định nghĩa:
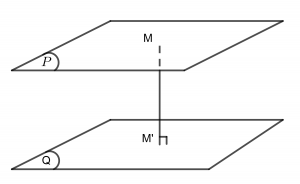
Trước hết, ta nhắc lại định nghĩa khoảng cách từ một điểm M lên mặt phẳng (P) là khoảng cách giữa M và hình chiếu của nó trên mặt phẳng (P). Ký hiệu là d(M,(P)).
Cho hai mặt phẳng (P) và (Q) song song với nhau. Khoảng cách giữa mặt phẳng (P) và (Q) là khoảng cách từ một điểm M bất kỳ trên mặt phẳng (P) đến mặt phẳng (Q) hoặc ngược lại. Ký hiệu là d((P),(Q)).
Bộ đề thi Online các dạng có giải chi tiết: Khoảng cách giữa 2 mặt phẳng
CÔNG THỨC TÍNH KHOẢNG CÁCH GIỮA HAI MẶT PHẲNG
Cho hai mặt phẳng (P), (Q) song song trong không gian. Phương trình của chúng đều có thể đưa về dạng:
(P): ax+by+cz+d=0 và (Q): ax+by+cz+d’=0 (a²+b²+c²>0 và d≠d’)
Khi đó giả sử M(α;β;γ) thuộc mặt phẳng (P) ta có: aα+bβ+cγ=-d. Khoảng cách giữa (P) và (Q) chính là khoảng cách giữa M và (Q). Do đó:
Vậy công thức tính khoảng cách giữa hai mặt phẳng song song là:
Vì vậy cách tính khoảng cách giữa hai mặt phẳng là ta biến đổi hai phương trình sao cho x, y, z có cùng hệ số sau đó mới áp dụng công thức (dòng màu xanh) bên trên.
VÍ DỤ TÍNH KHOẢNG CÁCH GIỮA 2 MẶT PHẲNG
Ví dụ:
Tính khoảng cách giữa hai mặt phẳng (P):x+2y+2z+3=0 và (Q): 2x+4y+4z-11=0.
Lời giải:
Bộ đề thi Online các dạng có giải chi tiết: Khoảng cách giữa 2 mặt phẳng
Ta còn chẳng cần phải tìm hình chiếu. Thật dễ dàng phải không nào :)) . Chúc các em thành công!
Xem thêm:
Phương trình mặt cầu và các dạng bài tập
Phương pháp tọa độ trong không gian
Khoảng cách từ điểm đến mặt phẳng trong không gian
Khoảng cách giữa đường thẳng và mặt phẳng hình Oxyz
Công thức tính khoảng cách giữa 2 điểm
Khoảng cách giữa 2 đường thẳng trong oxyz
Vị trí tương đối của 2 đường thẳng trong không gian
Công thức tính góc giữa 2 mặt phẳng
Khoảng cách từ điểm đến đường thẳng trong oxyz
Phương Pháp Tọa Độ Oxyz –