5/5 – (1 bình chọn)
Hình tam giác là hình học không gian, được áp dụng nhiều trong môn Toán hình cũng như ngoài đời sống. Hãy cùng nhau đọc bài viết dưới đây để tìm hiểu kỹ hơn về các phép tính chu vi tam giác đúng chuẩn sách giáo khoa nhé.
Hình tam giác là gì?
Muốn thực hiện được phép tính chu vi tam giác thì trước tiên ta phải hiểu rõ về hình tam giác là gì. Cần phân biệt rõ các tính chất, đặc điểm của chúng để kết hợp công thức tính toán cho đúng.
Hình tam giác
Hình tam giác là hình học không gian cơ bản, thường xuất hiện rộng rãi ở ngoài cuộc sống và trên sách giao khoa. Hình bao gồm 3 cạnh vẽ thành 3 đường thẳng nối với nhau ở các đình. Lưu ý 3 điểm được nối không thẳng hàng, không nằm trên một đường thẳng.
Tam giác là một hình đa giác đơn, hình đa giác có 3 cạnh là hình ít số cạnh nhất trong hình học không gian của đa giác.
Và tổng số góc trong cùng một hình tam giác có số đo góc là 180 độ.
Tham khảo thêm về các phép tính khác cho tam giác :
Các đặc điểm của hình tam giác
Sau khi hiểu được khái niệm về hình tam giác thì hãy bước sang giai đoạn tìm hiểu yếu tố tạo nên một hình tam giác bao gồm những gì. Từ đó có thể rút ra nhiều kết luận cho công thức tính chu vi tam giác.
Các góc trong cùng một tam giác thường được gọi là góc trong. Còn góc kề bù đối với góc trong tam giác thì gọi là góc ngoài của tam giác. Góc ngoài của tam giác thì bằng tổng tất cả các góc trong của tam giác nhưng mà không kề bù với góc ngoài. Mỗi tam giác sẽ có 6 góc ngoài, 3 góc trong.
Các đường đồng quy trong tam giác
Đường cao của tam giác:
Khi tính chu vi tam giác hay diện tích tam giác nếu như không có số đo của các cạnh cho trước thì bắt buộc chúng ta phải tìm ra đường cao để tìm chu vi hay diện tích cho hình tam giác.
Vì thế trong mỗi tam giác tối đa có 3 đường cao. Cả 3 đường cao đều quy tại một điểm trong hình tam giác thì điểm chung có tên gọi là trực tâm của hình tam giác.
Đường trung tuyến của tam giác:
Đường trung tuyến cũng góp phần quan trọng trong các phép tính chu vi tam giác hay tính thể tích, diện tích.
Đường trung tuyến là đoạn thẳng được kẻ từ đỉnh tam giác đến trung điểm của các cạnh đối diện.
Giống như đường cao, mỗi một tam giác chỉ tồn tại 3 đường trung tuyến. Khi cả 3 đường trung tuyến này đều đồng quy tại một điểm thì được có tên là trọng tâm trong hình tam giác.
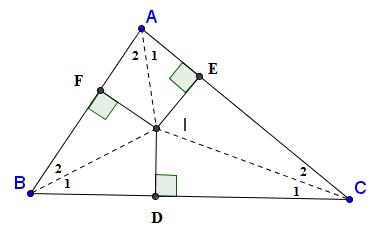
Các đường đồng quy trong tam giác
Khoảng cách tính từ điểm trọng tâm đến các cạnh của tam giác chỉ bằng 2/3 chiều dài những đường trung tuyến. Đường trung tuyến được chia thành 2 phần có tổng diện tích bằng nhau.
Đường trung trực của tam giác:
Đường trung trực của hình tam giác thường là đường thẳng luôn vuông góc với cạnh nào đó tại trung điểm.
Mỗi một hình tam giác cũng chỉ có 3 đường trung trực. Nếu như cả 3 đường trung trực đều đồng quy tại cùng một điểm thì điểm đó được gọi là tâm điểm của đường tròn năm ngoại tiếp với hình tam giác. Và điểm tâm đó đều lần lượt thành 3 đỉnh trong hình tam giác.
Đường phân giác trong tam giác:
Đường phân giác là đường thẳng được kẻ từ đỉnh điểm đến các cạnh đối diện, chúng chia đều tại đỉnh là thành 2 phần có số đo bằng nhau.
Mỗi hình tam giác cũng chỉ có 3 đường phân giác. Nếu cả 3 đường đều đồng quy tại cùng một điểm thì cũng được gọi là tâm đường tròn nhưng nội tiếp tam giác. Khoảng cách tâm đến các cạnh tam giác bằng nhau.
Tổng hợp công thức tính chu vi tam giác:
Dưới đây sẽ là phẩn tổng hợp các công thức tính chu vi tam giác được áp dụng vào từng loại tam giác riêng biệt như tam giác thường, tam giác vuông, tam giác đều,…
Công thức tính chu vi tam giác chung
Chu vi tam giác thường được xác định bởi chiều dài của tổng 3 cạnh trong tam giác.
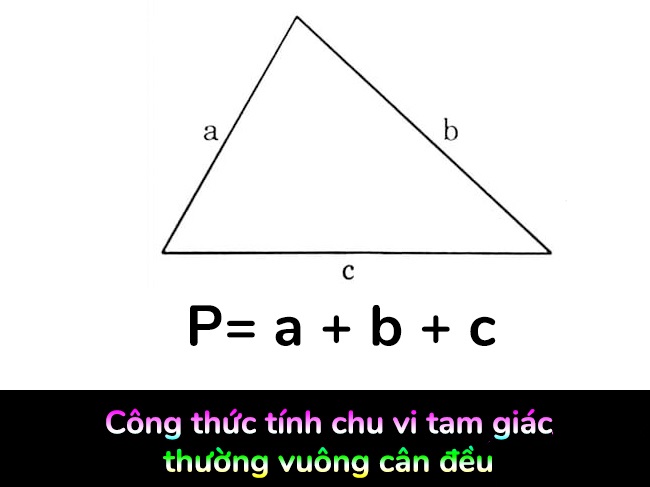
Công thức tính chu vi tam giác được thể hiện như sau:
P= a + b + c
Công thức tính chu vi tam giác chung
Chú thích :
-
P sẽ là ký hiệu đại diện cho
chu vi tam giác
thường
-
a,b. c lần lượt là 3 cạnh trong hình tam thường
Đồng thời dựa vào cách tính trên, chúng ta đã cho ra cách tính được nửa chu vi tam giác như sau:
½ P = 2 : ( a + b +c )
Công thức tính chu vi tam giác cân là gì?
Trước tiên phải hiểu được khái niệm về tam giác cân là gì rồi mới bắt đầu áp dụng công thức.
Tam giác cân là hình có 2 góc luôn bằng nhau đồng thời 2 canh trong tam giác cũng bằng nhau. Đỉnh tam giác cân sẽ là giao điểm cho cả 2 cạnh kề bên. Để xác định được chu vi tam giác cân thì cần phải biết 2 cạnh của hình và đỉnh tam giác.
Công thức tính toán chu vi tam giác dạng cân được thể hiện như sau:
P = 2 a + c
Chú thích:
-
P là ký hiệu cho
chu vi tam giác
cân
-
a lần lượt là 2 cạnh kề bên trong hình tam giác cân
-
c sẽ là cạnh đáy của hình tam giác giác cân
Công thức áp dụng cho chu vi tam giác vuông là gì?
Khái niệm về tam giác vuông khá đơn giản. Tam giác vuông là hình có một góc vuông 90 độ.
Công thức áp dụng cho phép tính chu vi tam giác vuông như sau:
P = a + b + c
Tam giác vuông
Chú thích:
-
P vẫn là ký hiệu cho
chu vi tam giác
vuông
-
a lẫn b sẽ là hai cạnh lần lượt trong tam giác vuông
-
c được xem là cạnh huyền trong tam giác vuông
Công thức cho phép tính chu vi tam giác đều là gì?
Khái niệm tam giác đều có thể hiểu là hình tam giác có 3 cạnh đều bằng nhau. Như vậy muốn tính chu vi tam giác đều ta cần phải biết chiều dài của 1 cạnh tam giác. Vì chiều dài 3 cạnh không khác nhau nên ta có công thức tính chu vi tam giác như sau:
P = a x 3 = b x 3= c x 3
Chú thích :
-
P là ký hiệu
chu vi tam giác
đều
-
a, b và c lần lươt là các cạnh bất kỳ nào đó của tam giác đều
Bài tập nào áp dụng cho công thức tính chu vi tam giác?
Ví dụ số 1: bài toán có hình tam giác BCD lần lượt cho chiều dài các cạnh như sau: a = 4cm, b= 5cm, c= 6cm. Áp dụng công thức để tìm ra chu vi tam giác BCD?
Bài giải:
Chu vi tam giác BCD là:
Công thức: P = a + b + c
P = 4 + 5 + 6 = 15cm
Đáp án chu vi tam giác BCD = 15cm
Làm nhiều bài tập để ghi nhớ công thức
Ví dụ số 2: Bài toán cho tam giác BCD cân, có các cạnh a bằng 6 cm, c bằng 8. Hỏi chu vi tam giác BCD là bao nhiêu?
Bài giải
Chu vi tam giác đều BCD là:
Công thức tính : P = 2a + c
P = 2 x (6 + 8) = 96cm
Kết quả chu vi tam giác cân BCD = 96cm
Ví dụ số 3 : bài toán cho hình tam giác đều BCD, có các cạnh lầ lượt là a = 3cm, b= 3cm, c= 3cm. Tính chu vi tam giác đều BCD
Bài giải:
Chu vi tam giác đều BCD là:
Công thức tính chu vi tam giác đều: P = a x 3 = b x 3= c x 3
P= 3 x 3 = 9cm
Kết quả cho chu vi của tam giác đều BCD có 3 cạnh bằng nhau = 9cm
Bài viết trên đây đã cho chúng ta ôn lại các kiến thức tính chu vi cơ bản nhất của hình tam giác. Hy vọng bài viết có thể đem lại nhiều thông tin bổ ích cho các bạn đọc. Hình học không gian không chỉ áp dụng trên sách giáo khoa mà chúng còn phổ biến trong thế giới đời thực.