Cách tính Chu vi và Diện tích của hình thang (có ví dụ dễ hiểu)
Tiếp nối chuyên mục Toán học, hôm nay mình sẽ hướng dẫn các bạn cách để TÍNH CHU VI HÌNH THANG và TÍNH DIỆN TÍCH HÌNH THANG một cách đơn giản và dễ hiểu nhất.
Trên thực tế, chúng ta khá ít gặp các bài toán chỉ yêu cầu tính diện tích đơn thuần, hoặc là cung cấp sẵn đầy đủ các yếu tố chỉ cần áp vào công thức. Mà thay vào đó, thường chúng ta sẽ phải đi tìm hoặc đó chỉ là một bài toán trung gian.
Tuy nhiên, với mục đích là giúp các bạn ghi nhớ và hiểu sâu sắc công thức nên những ví dụ mà mình lựa chọn khá là đơn giản. Mục đích chính là giúp bạn ghi nhớ công thức hơn !
Ngoài ra mình cũng lồng ghép thêm một số kiến thức khác có liên quan đến hình thang, như tính chất hình thang, đường trung bình của hình thang để các bạn có thể vận dụng làm bài tốt hơn.
#1. Hình thang là gì?
Nếu một tứ giác có hai cạnh đối diện song song thì tứ giác đó được gọi là hình thang. Đơn giản ha !
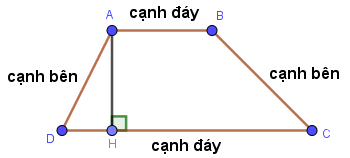
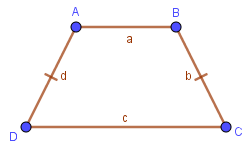
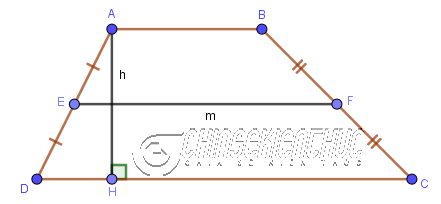
Ví dụ tứ giác ABCD có AB // DC thì tứ giác này là một hình thang, hình thang ABCD có:
- AB, DC là các cạnh đáy
- AD, BC là các cạnh bên
- AH là chiều cao kẻ từ A đến DC
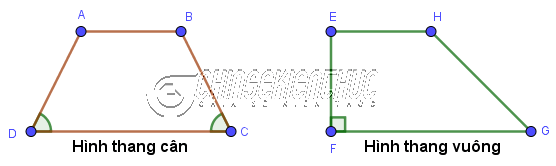
Hình thang cân là một hình thang có hai góc kề một đáy bằng nhau.
Hình thang vuông là một hình thang có một góc bằng 90o.
#2. Hình thang có tình chất gì?
- Hai cạnh bên trong một hình thang cân có độ dài bằng nhau.
- Hai đường chéo trong một hình thang cân có độ dài bằng nhau.
- Độ dài đường trung bình của hình thang bằng một phần hai độ dài tổng của hai cạnh đáy.
#3. Cách tính chu vi hình thang (công thức & ví dụ)
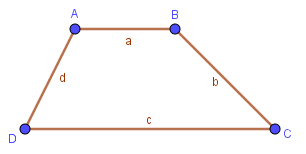
Chu vi của hình thang bằng tổng độ dài các cạnh của hình thang. Cụ thể thì công thức như sau:
Công thức tính chu vi hình thang: $C_{ABCD}=a+b+c+d$
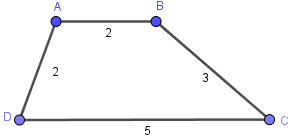
Ví dụ 1. Cho hình thang ABCD có AB=2, BC=3, CD=5, DA=2. Tính chu vi hình thang ABCD
Áp dụng công thức $C_{ABCD}=a+b+c+d$ vào hình thang ABCD ta được $2+3+5+2=12$
=> Vậy chu vi của hình thang đã cho là 12
Đặc biệt, Chu vi của hình thang cân bằng 2 lần độ dài cạnh bên + với tổng của hai cạnh đáy
Công thức tính chu vi hình thang cân: $C_{ABCD}=2d+(a+c)$ hoặc $C_{ABCD}=2b+(a+c)$
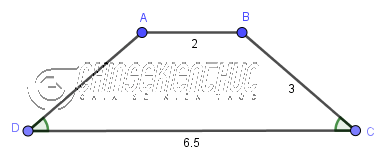
Ví dụ 2. Cho hình thang ABCD có $AB=2, BC=3, CD=6.5$ và $\widehat{ADC}=\widehat{BCD}$
Lời Giải:
Hình thang ABCD có góc $\widehat{ADC}=\widehat{BCD}$ nên hình thang ABCD là một hình thang cân
Áp dụng công thức $C_{ABCD}=2b+(a+c)$ vào hình thang ABCD ta được $2 \times 3+(2+6.5)=14.5$
=> Như vậy chu vi của hình thang đã cho là 14.5
#4. Cách tính diện tích hình thang (công thức & ví dụ)
Tùy vào từng bài toán cụ thể mà chúng ta sẽ lựa chọn và áp dụng công thức sao cho phù hợp nhất.
Trong bài viết này mình sẽ trình bày với bạn công thức tính diện tích của hình thang (thường), hình thang khi biết đường trung bình và hình thang cân.
4.1. Trường hợp 1: Tính diện tích hình thang khi biết độ dài hai cạnh đáy và chiều cao
Diện tích của hình thang bằng tích của một phần hai, tổng của hai cạnh đáy, chiều cao.
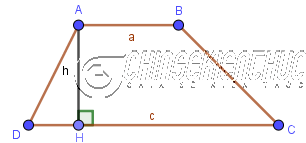
Ta có được công thức: $S_{ABCD}=\frac{1}{2}.(a+c).h$
Ví dụ 3. Cho hình thang ABCD biết AB=2, DC=5, AH=3. Tính diện tích của hình thang ABCD
Lời Giải:
Áp dụng công thức $S_{ABCD}=\frac{1}{2}.(a+c).h$ vào hình thang ABCD ta được $\frac{1}{2}.(AB+DC).AH=\frac{1}{2}.(2+5).3=10.5$
=> Vậy diện tích của hình thang đã cho là 10.5 ĐVDT
4.2. Trường hợp 2: Tính diện tích hình thang khi biết độ dài đường trung bình và chiều cao
Diện tích của hình thang sẽ bằng tích đường trung bình, chiều cao
Công thức: $S_{ABCD}=m.h$
Chú ý: Vì m là đường trung bình của hình thang ABCD nên $m=\frac{1}{2}(AB+DC)$
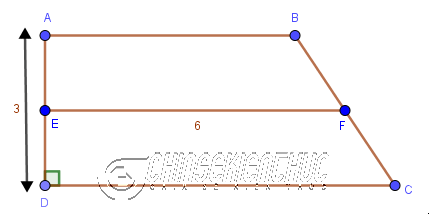
Ví dụ 4: Cho hình thang ABCD có $DA=3$; E, F lần lượt là trung điểm AD, BC; $EF=6; \widehat{ADC}=90^o$. Tính diện tích hình thang ABCD
Lời Giải:
Trước hết chúng ta nhận xét rằng hình thang ABCD là hình thang vuông, AD là đường cao, EF là đường trung bình
Áp dụng công thức $S_{ABCD}=m.h$ vào hình thang ABCD ta được $S_{ABCD}=EF.AD=6.3=18$
=> Vâng, như vậy diện tích hình thang đã cho là 18 ĐVDT
#5. Cách tính diện tích hình thang cân
Diện tích hình thang cân sẽ được tính theo công thức: $S_{ABCD}=EA(DE+AB)$
Thật vậy
Dựng đường cao BF
$S_{ABCD}=S_{DEA}+S_{ABFE}+S_{CFB}$
$=\frac{1}{2}.DE.EA+EA.AB+\frac{1}{2}.CF.FB$
Vì $DE=CF, EA=FB$ nên
$=\frac{1}{2}.DE.EA+EA.AB+\frac{1}{2}.DE.EA$
$=DE.EA+EA.AB$
$=EA.(DE+AB)$
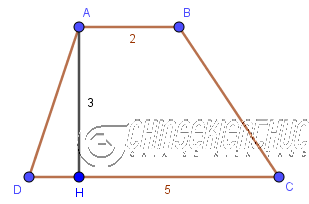
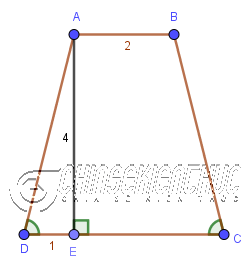
Ví dụ 5: Cho hình thang ABCD có $AB=2, AE \bot DC, ED=1, EA=4$, $\widehat{ADC}=\widehat{BCD}$. Tính diện tích hình thang ABCD
Lời Giải:
Hình thang ABCD là hình thang cân vì $\widehat{ADC}=\widehat{BCD}$
Áp dụng công thức $S_{ABCD}=EA.(DE+AB)$ vào hình thang ABCD ta được $4(1+2)=12$
=> Vậy diện tích của hình thang đã cho là 12 ĐVDT
#6. Lời kết
Như vậy là trong bài viết này mình đã giới thiệu đến các bạn tất cả năm công thức tính diện tích và chu vi hình thang rồi nhé (2 công thức tính chu vi hình thang và 3 công thức tính diện tích hình thang).
Tùy thuộc vào giả thuyết của bài toán đưa ra mà chúng ta sẽ cân nhắc, lựa chọn công thức cho phù hợp. Khi chọn được cộng thức phù hợp sẽ giúp bạn tiết kiệm được khá nhiều thời gian, công sức, không phải giải vòng vòng mất thời gian và đôi khi còn bị sai.
Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo ha !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Bài viết đạt: 5/5 sao – (Có 1 lượt đánh giá)