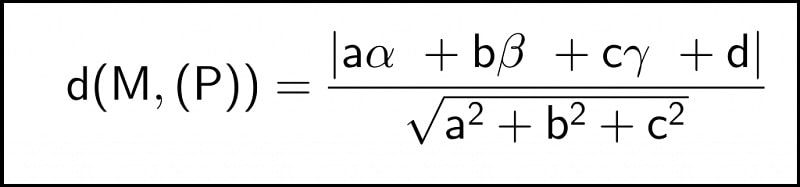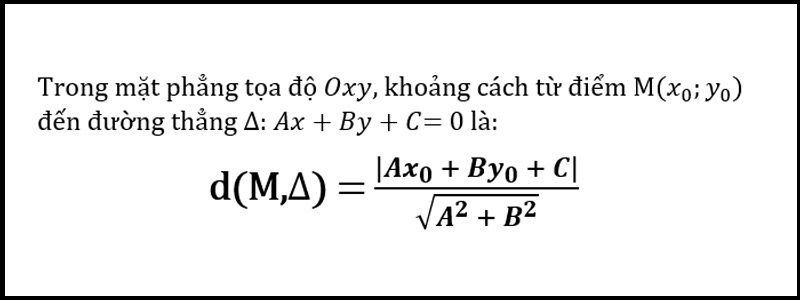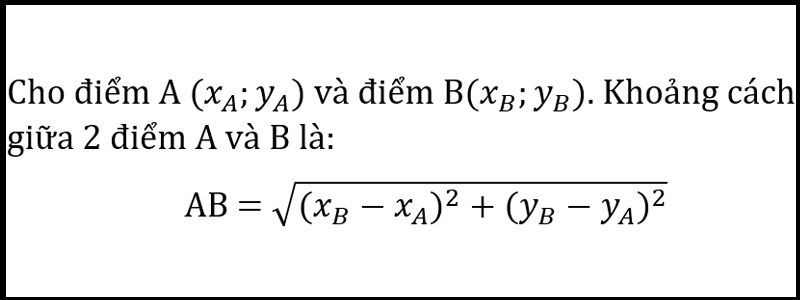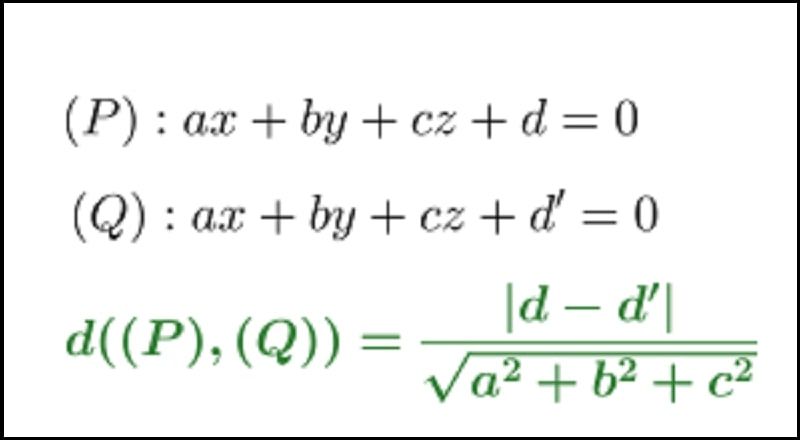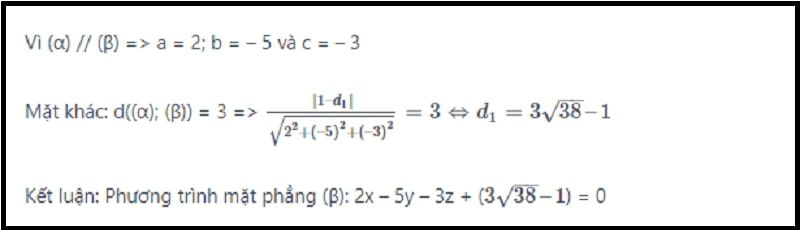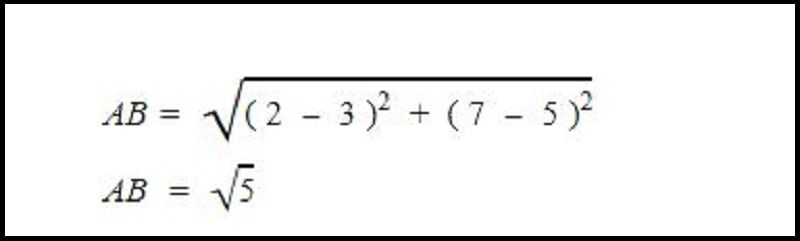Công thức tính khoảng cách giữa hai điểm đến mặt phẳng, từ điểm đến đường thẳng, khoảng cách 2 điểm,… được sử dụng phổ biến trong hình học không gian. Bài viết dưới đây sẽ giúp bạn tổng hợp tất cả các công thức tính khoảng cách thông dụng hiện nay. Hãy lưu lại các công thức và áp dụng ngay nhé!
Khái niệm công thức tính khoảng cách
Trong khoa học, công thức là một hình thức trình bày thông tin chính xác dưới dạng các biểu tượng. Theo đó công thức tính khoảng cách là tập hợp những cách thức dùng để tính khoảng cách từ vị trí này đến vị trí khác. Ví dụ tính khoảng cách giữa hai điểm hoặc khoảng cách giữa hai mặt phẳng.
Công thức tính khoảng cách thường được ứng dụng nhiều ở trong hình học phẳng và hình học không gian. Có nhiều dạng công thức tính khoảng cách khác nhau, học sinh có thể linh hoạt áp dụng công thức phù hợp để giải bài tập cho ra đáp án đúng.
Các công thức tính khoảng cách
Sau đây là tổng hợp những công thức tính khoảng cách được sử dụng nhiều nhất. Bạn còn chờ đợi gì mà không lưu lại ngay để việc tính toán trở nên đơn giản và dễ dàng hơn bao giờ hết.
Công thức tính khoảng cách từ điểm đến mặt phẳng
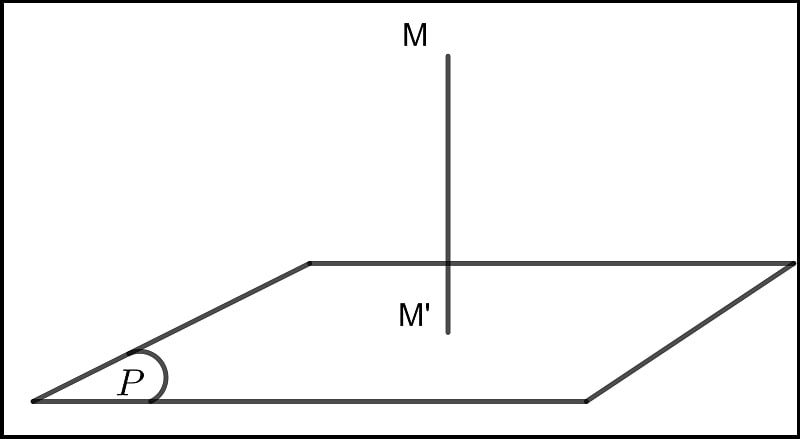
Κhοảng cách từ 1 điểm A đến mặt phẳng (P) được định nghĩa là khοảng cách từ điểm A đến hình chiếu (vuông góc) của nó trên (P). Ký hiệu là d(M,(P)). Như vậy để tính khοảng cách từ điểm M đến mặt phẳng (P) ta cần tìm hình chiếu của điểm đó trên mặt phẳng (P). Tuy nhiên, các bạn sẽ tính được khoảng cách dễ dàng hơn nếu áp dụng công thức sau:
Trong không gian Oxyz, cho điểm M(α;β;γ) cùng mặt phẳng (P): ax+by+cz+d=0. Theo đó, ta có công thức khoảng cách từ điểm M đến mặt phẳng (P): ax+by+cz+d=0 đã cho là:
Công thức tính khoảng cách từ điểm đến đường thẳng
Cho đường thẳng d: ax + by + c = 0 và điểm N (x0; y0). Khi đó khoảng cách từ điểm N đến đường thẳng d là d(N; d).
Chú ý: Trong trường hợp đường thẳng d nêu ở ví dụ trên chưa viết dưới dạng tổng quát. Trước khi áp dụng công thức, đầu tiên ta cần đưa đường thẳng d về dạng tổng quát y=ax+b
Công thức tính khoảng cách giữa hai đường thẳng
Trong không gian hai đường thẳng có 4 vị trí tương đối là: trùng nhau; Song song; Chéo nhau và cắt nhau. Trường hợp 2 đường thẳng trùng nhau hoặc cắt nhau đều có thể xem khoảng cách giữa chúng bằng 0.
Tuy nhiên, nếu 2 đường thẳng song song, chéo nhau, chúng ta vẫn có thể tính khoảng cách giữa chúng. Khoảng cách giữa 2 đường thẳng sẽ bằng khoảng cách từ điểm bất kỳ trên đường thẳng này đến đường thẳng kia.
Công thức tính khoảng cách giữa hai điểm
Tính khoảng cách giữa 2 điểm bất kì chính là tìm ra độ dài đoạn thẳng nối liền 2 điểm đã được cho trước (hoặc đã xác định trước). Tuy nhiên bạn cần lưu ý rằng, khoảng cách (độ dài nối liền) giữa 2 điểm bất kỳ không phải là độ dài đường thẳng và cũng không phải độ dài đoạn thẳng vuông góc nào khác.
Dựa trên các cơ sở trên, chúng ta sẽ có công thức tính khoảng cách giữa 2 điểm bất kỳ như sau:
Công thức tính khoảng cách giữa hai mặt phẳng
Chúng ta sẽ dễ dàng tính được khoảng cách giữa 2 mặt phẳng song song khi biết trước phương trình của 2 mặt phẳng đó. Sau đây là công thức tính khoảng cách giữa hai mặt phẳng song song.
Công thức tính khoảng cách trong không gian sẽ rất dễ áp dụng nếu bạn hiểu bản chất vấn đề. Nhìn chung chỉ có một số công thức nhất định, từ gợi ý ban đầu bạn có thể giải ra ngay đáp án.
Các bài tập tính khoảng cách cơ bản có lời giải
Trên đây là 5 công thức tính khoảng cách quan trọng trong toán học. Để có thể ghi nhớ và áp dụng thành thạo, bạn hãy thực hành giải ngay một số bài tập cơ bản dưới đây.
Bài tập 1
Trong không gian Oxyz, có hai mặt phẳng có phương trình lần lượt là
(α): x – 2y + z + 1 = 0
(β): x – 2y + z + 3 = 0.
Yêu cầu hãy tính khoảng cách giữa 2 mặt phẳng (α) và (β)?
Hướng dẫn:
Bài tập 2
Hai mặt phẳng (α) // (β), cách nhau 3 cm. Ta đã biết phương trình của mỗi mặt phẳng lần lượt là
(α): 2x – 5y – 3z + 1 = 0
(β): ax + by + cz + d2 = 0
Yêu cầu hãy xác định các hệ số a, b, c của phương trình mặt phẳng (β).
Hướng dẫn:
Bài tập 3
Trong mặt phẳng Oxy, cho 2 điểm lần lượt có tọa độ là A (3; 5) và điểm B (2; 7). Hãy xác định độ dài đoạn thẳng AB trong mặt phẳng tọa độ Oxy đã cho. Khi đó ta có độ dài nối liền 2 điểm A và B chính là khoảng cách giữa 2 điểm A và B.
Hướng dẫn:
Xem thêm:
Tin chắc bài viết trên đã giúp bạn hiểu rõ hơn và biết được công thức tính khoảng cách giữa các điểm, đường thẳng và mặt phẳng trong không gian. Hy vọng qua bài viết này bạn sẽ nhớ chính xác công thức, biết cách áp dụng thành thạo hơn khi giải bài tập. Chúc bạn học thật tốt nhé!