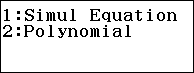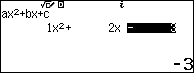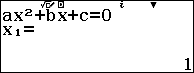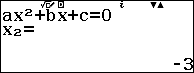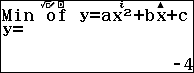Mến chào tất cả các bạn, hôm này mình sẽ hướng dẫn cho các bạn cách giải phương trình bậc hai bất kì bằng 7 cách khác nhau. Tha hồ cho các bạn chọn lựa.
Mỗi một cách sẽ có một số ưu điểm và khuyết điểm riêng, tùy thuộc vào phương trình cụ thể mà chúng ta sẽ cân nhắc lựa chọn sử dụng cho phù hợp. Hãy linh hoạt nha các bạn !
Trong 7 cách này có cách chỉ có thể áp dụng cho phương trình bậc hai, có cách có thể áp dụng cho phương trình bậc 2, 3, 4. Đặc biệt, có cách có thể áp dụng cho phương trình bậc n.
Okay, ngay bây giờ chúng ta cùng tìm hiểu thôi nào …
I. Định nghĩa phương trình bậc hai
Phương trình bậc hai là phương trình có dạng $ax^2+bx+c=0$ với điều kiện là $a \neq 0$
Phương trình $x^2+2x-3=0$ là một phương trình bậc hai
II. 7 cách giải phương trình bậc hai
#1. Tính biệt thức Delta
Đây là phương pháp được nhiều người sử dụng nhất, việc áp dụng rất đơn giản, bạn chỉ cần nhớ công thức là được thôi.
Lời Giải:
$\Delta=b^2-4.a.c=2^2-4.1.(-3)=16$
Vì $\Delta>0$ nên phương trình đã cho có hai nghiệm phân biệt:
- $x_1=\frac{-b+\sqrt{\Delta}}{2.a}=\frac{-2+\sqrt{16}}{2.1}=1$
- $x_2=\frac{-b-\sqrt{\Delta}}{2.a}=\frac{-2-\sqrt{16}}{2.1}=-3$
=> Vậy phương trình đã cho có hai nghiệm phân biệt là 1, -3
Chú ý:
- $\Delta=0$ thì phương trình có nghiệm kép $x_1=x_2=\frac{-b}{2a}$
- $\Delta<0$ thì phương trình vô nghiệm
#2. Tính biệt thức Delta’
Phương pháp này nên được sử dụng khi b là một số nguyên chẵn, tức là b có dạng $b=2b’$
Phương pháp này rất có ích khi các hệ số a, b, c có giá trị lớn.
Lời Giải:
Dễ thấy $b’=\frac{b}{2}$ hay $b’=\frac{2}{2}=1$
$\Delta’=b’^2-a.c=1^2-1.(-3)=4$
Vì $\Delta’ > 0$ nên phương trình đã cho có hai nghiệm phân biệt
- $x_1=\frac{-b+\sqrt{\Delta’}}{2}=\frac{-1+\sqrt{4}}{1}=1$
- $x_2=\frac{-b-\sqrt{\Delta’}}{2}=\frac{-1-\sqrt{4}}{1}=-3$
Vậy phương trình đã cho có hai nghiệm phân biệt là 1, -3
Chú ý:
- $\Delta’=0$ thì phương trình có nghiệm kép $x_1=x_2=\frac{-b’}{a}$
- $\Delta’<0$ thì phương trình vô nghiệm
#3. Hệ quả của định lý Viète
Phương pháp này nếu áp dụng được sẽ giúp chúng ta tiết kiệm được khá nhiều thời gian và công sức để giải bài, tuy nhiên việc áp dụng trong thực tế khá hạn chế.
Lời Giải:
Vì $a+b+c=0$ hay $1+2+(-3)=0$ nên phương trình đã cho có một nghiệm là 1 và nghiệm còn lại là $\frac{c}{a}=\frac{-3}{1}=-3$
=> Vậy phương trình đã cho có hai nghiệm phân biệt là 1, -3
Chú ý: Nếu $a-b+c=0$ thì phương trình có một nghiệm là -1 và nghiệm còn lại là $-\frac{c}{a}$
#4. Nhẩm nghiệm
Trước hết các bạn nên nhớ đa thức $f(x)=ax^2+bx+c$ với điều kiện $a \neq 0$ và $a, b, c$ là những số nguyên
-
Nếu có nghiệm nguyên thì những nghiệm nguyên này phải là ước của c
-
Nếu có nghiệm hữu tỉ $\frac{p}{q}$ thì p phải là ước của c và q phải là ước của a
Thực ra phương pháp này là trường hợp mở rộng của phương pháp hệ quả của định lý Viète bên trên.
Lời Giải:
Vì $a=1, b=2, c=-3$ là những số nguyên nên chúng ta có thể áp dụng phương pháp này:
Đặt $f(x)=x^2+2x-3$
-3 có các ước -1, 1, -3, 3
Nếu phương trình có nghiệm nguyên thì chỉ có thể là các số -1, 1, -3, 3
- $f(-1)=(-1)^2+2(-1)-3=-4 \neq 0$ suy ra -1 không là nghiệm của phương trình đã cho
- $f(1)=(1)^2+2(1)-3=0$ suy ra 1 là nghiệm của phương trình
- $f(-3)=(-3)^2+2(-3)-3=0$ suy ra -3 là nghiệm của phương trình
=> Vậy phương trình đã cho có hai nghiệm phân biệt là 1, -3
Chú ý: Vì phương trình bậc hai có tối đa hai nghiệm nên mình không cần kiểm tra 3 (3 chắc chắn không phải là nghiệm của phương trình đã cho)
#5. Phương pháp đồ thị
Phương pháp đồ thị có thể áp dụng được cho phương trình bậc 2, 3 và 4. Điều kiện là bạn phải vẽ được đồ thị của chúng.
Ngoài ra, phương pháp này chỉ khả dụng khi nghiệm là những số nguyên.
Lời Giải:
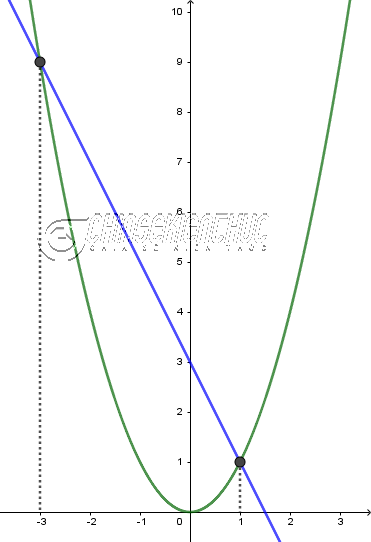
Phương trình đã cho tương được với $x^2=-2x+3$
Đặt $f(x)=x^2$ và $g(x)=-2x+3$
Vẽ f(x) và g(x) trên cùng một hệ trục tọa độ.
Hoành độ giao điểm của đồ thị hàm số f(x) và g(x) chính là nghiệm của phương trình đã cho.
Quan sát đồ thị ta dễ dàng nhận thấy hoành độ của hai giao điểm lần lượt là 1 và -3
Dự đoán 1 và -3 là nghiệm của phương trình
Thay 1 và -3 lần lượt vào phương trình đã cho $1^2+2.1-3=0$ và $(-3)^2+2.(-3)-3=0$ (thỏa mãn)
=> Vậy phương trình đã cho có hai nghiệm phân biệt là 1, -3
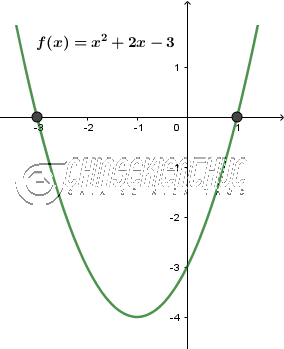
Chú ý: Ở đây mình chọn cách này để học sinh Trung học cơ sở vẫn có thể hiểu được. Trường hợp bạn có thể vẽ được đồ thị của hàm số bậc hai dạng đầy đủ tức $ax^2+bx+c$ thì bạn không cần phải vẽ hai đồ thị.
Lúc bấy giờ hoành độ giao điệm của đồ thị với trực hoành chính là nghiệm của phương trình.
#6. Phương pháp máy tính CASIO fx-580VN X
Như mình đã nói bên trên, phương pháp này chỉ nên sử dụng khi cần kiểm tra kết quả hoặc làm bài kiểm tra / bài thi trắc nghiệm
Lời Giải:
Bước 1. Chọn phương thức tính toán Equation / Func
Bước 2. Chọn Polynomial
Bước 3. Chọn bậc 2 (vì chúng ta đang giải phương trình bậc 2)
Bước 4. Lần lượt nhập các hệ số …
Bước 5. Nhấn phím = ta thu được nghiệm thứ nhất, tiếp tục nhấn phím = ta thu được nghiệm thứ 2
Nếu tiếp tục nhấn phím = ta sẽ thu được hoành độ và trung độ của điểm cực tiểu.
Chú ý: Nhắc lại lần nữa, phương pháp này có thể tìm được nghiệm của phương trình bậc 2, 3 và 4 nha các bạn.
#7. Phương pháp biến đổi tổng quát
Phương pháp này chủ yếu để rèn luyện khả năng tư duy, tính toán, tìm nghiệm trong trường hợp tổng quát, biện luận nghiệm, …
Lời Giải:
$x^2+2x-3=0 \Leftrightarrow \left(\frac{x^2}{x}+\frac{2x}{2x}\right)^2-\left(\frac{2x}{2x}\right)^2-3=0 \Leftrightarrow (x+1)^2-(1)^2-3=0 \Leftrightarrow (x+1)^2=4$
$\Leftrightarrow \sqrt{(x+1)^2}= \sqrt{4} \Leftrightarrow |x+1|=2$
$\Leftrightarrow \left[\begin{array}{}x+1=2 \\ x+1=-2 \end{array}\right. \Leftrightarrow \left[\begin{array}{}x=1 \\ x=-3 \end{array}\right.$
Chú ý:
- $x=0$ không là nghiệm của phương trình
- Cẩn thận sai sót khi $a \neq 1$
III. Lời kết
Vâng, trên đây là 7 cách giải phương trình bậc 2 mà mình đã tổng hợp lại cho các bạn tiện theo dõi. Hãy linh hoạt để áp dụng, nó sẽ giúp bạn tiết kiệm rất nhiều thời gian làm bài tập đấy.
- Nếu là một phương trình bậc 2 bất kỳ thì bạn nên ưu tiên sử dụng phương pháp 1.
- Nếu rơi vào các trường hợp đặc biệt thì ưu tiên sử dụng phương pháp 2, 3 và 4.
- Phương pháp đồ thị chỉ nên sử dụng khi cần biện luận nghiệm của phương trình.
- Phương pháp sử dụng máy tính Casio chỉ nên sử dụng để kiểm tra kết quả.
- Phương pháp 3 và 4 có thể áp dụng tương tự được cho phương trình bậc
n.
Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
Đọc thêm:
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Bài viết đạt: 5/5 sao – (Có 2 lượt đánh giá)