[ Công thức tính diện tích hình tam giác ] Tam giác thường, vuông, cân, đều
Toán Học
[ Công thức tính diện tích hình tam giác ] Tam giác thường, vuông, cân, đều
Công thức tính diện tích hình tam giác thường, vuông, cân, đều là một công thức rất phổ biến trong mỗi bài thi. Sau đây chúng tôi sẽ nêu ra những công thức tính diện tích tam giác trong bài viết sau đây.
Xem ngay : Công thức tính chu vi – Công thức tính diện tích hình chữ nhật
Công thức tính diện tích hình tam giác thường, vuông, cân, đều
– Các công thức tính diện tích tam giác, đầu tiên bạn bạn cần xác định loại tam giác đó là gì, từ đó tìm ra công thức tính diện tích chính xác nhất. Hiện tại, các loại tam giác phổ biến được chia thành 7 dạng chính như sau:
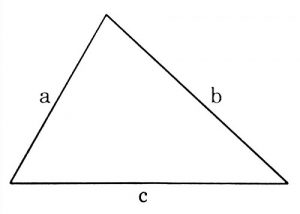
- Tam giác thường: Tam giác là đa giác lồi có 3 cạnh với 3 đỉnh nối 3 cạnh bên không thẳng hàng. Tổng các góc trong tam giác bằng 180°
- Tam giác vuông: là tam giác có 1 góc bằng 90°
- Tam giác cân: là tam giác có hai cạnh bên bằng nhau, 2 góc kề cạnh đáy bằng nhau.
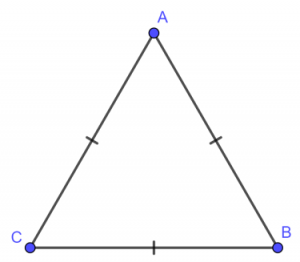
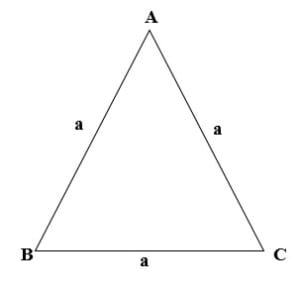
- Tam giác đều: là tam giác có 3 cạnh bên bằng nhau, 3 góc bằng nhau và bằng 60°
- Tam giác vuông cân: là tam giác có 1 góc bằng 90°, 2 cạnh bên bằng nhau, 2 góc đáy bằng 45°.
- Tam giác tù: là tam giác có 1 góc lớn hơn 90°
- Tam giác nhọn: là tam giác có ba góc trong tam giác nhỏ hơn 90°
Khái niệm về hình tam giác
– Tam giác hay hình tam giác là một loại hình cơ bản trong hình học: hình hai chiều phẳng có ba đỉnh là ba điểm không thẳng hàng và ba cạnh là ba đoạn thẳng nối các đỉnh với nhau.
– Tam giác là đa giác có số cạnh ít nhất (3 cạnh). Tam giác luôn luôn là một đa giác đơn và luôn là một đa giác lồi (các góc trong luôn nhỏ hơn 180o).
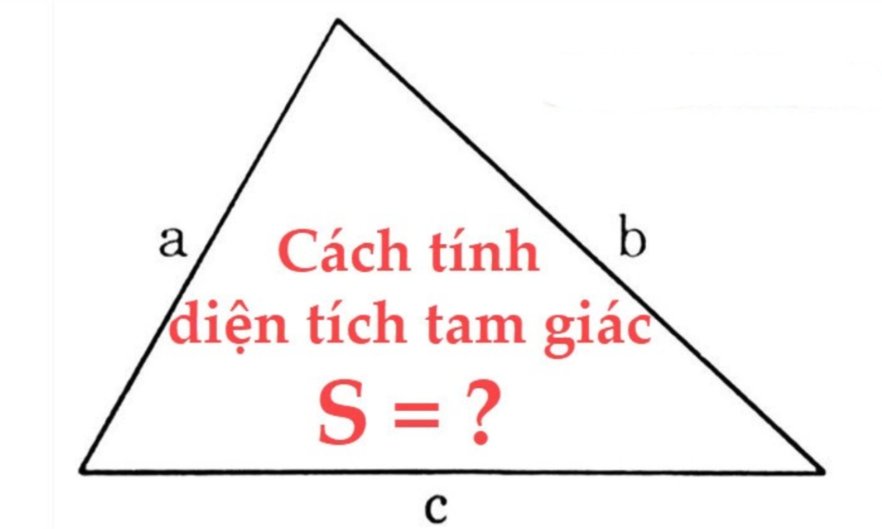
Công thức tính diện tích tam giác thường
+ Diện tích tam giác thường được tính bằng cách nhân chiều cao với độ dài đáy, sau đó tất cả chia cho 2. Nói cách khác, diện tích tam giác thường sẽ bằng 1/2 tích của chiều cao và chiều dài cạnh đáy của tam giác.
+ Đơn vị: cm2, m2, dm2, ….
S = (a x h) / 2
Trong đó :
- a: Chiều dài đáy tam giác (đáy là một trong 3 cạnh của tam giác tùy theo quy đặt của người tính)
- h: Chiều cao của tam giác, ứng với phần đáy chiếu lên (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy, đồng thời vuông góc với đáy của một tam giác)
Công thức suy ra :
h = (S x 2) / a hoặc a = (S x 2) / h
Xem ngay : Công thức tính chu vi hình tam giác
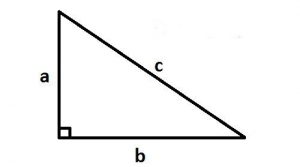
Công thức tính diện tích tam giác vuông
– Công thức tính diện tích tam giác vuông tương tự với cách tính diện tích tam giác thường, đó là bằng1/2 tích của chiều cao với chiều dài đáy.
– Mặc dù vậy hình tam giác vuông sẽ khác biệt hơn so với tam giác thường do thể hiện rõ chiều cao và chiều dài cạnh đáy, và bạn không cần vẽ thêm để tính chiều cao tam giác.
S = (A X H) /
– Công thức tính diện tích tam giác vuông tương tự với cách tính diện tích tam giác thường, đó là bằng1/2 tích của chiều cao với chiều dài đáy. Vì tam giác vuông là tam giác có hai cạnh góc vuông nên chiều cao của tam giác sẽ ứng với một cạnh góc vuông và chiều dài đáy ứng với cạnh góc vuông còn lại
S = (a x b)/ 2
=> Trong đó a, b: độ dài hai cạnh góc vuông
Công thức suy ra:
a = (S x 2) : b hoặc b = (S x 2) : a
Xem ngay : Đường trung tuyến trong tam giác
Công thức tính điện tích tam giác cân
– Tam giác cân là tam giác trong đó có hai cạnh bên và hai góc bằng nhau. Trong đó cách tính diện tích tam giác cân cũng tương tự cách tính tam giác thường, chỉ cần bạn biết chiều cao tam giác và cạnh đáy.
– Diện tích tam giác cân bằng Tích của chiều cao nối từ đỉnh tam giác đó tới cạnh đáy tam giác, sau đó chia cho 2.
S = (A X H)/ 2
=> Trong đó:
- a: Chiều dài đáy tam giác cân (đáy là một trong 3 cạnh của tam giác)
- h: Chiều cao của tam giác (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy).
Công thức tính diện tích tam giác đều
– Tam giác đều là tam giác có 3 cạnh bằng nhau. Trong đó cách tính diện tích tam giác đều cũng tương tự cách tính tam giác thường, chỉ cần bạn biết chiều cao tam giác và cạnh đáy.
– Diện tích tam giác cân bằng Tích của chiều cao nối từ đỉnh tam giác đó tới cạnh đáy tam giác, sau đó chia cho 2.
S = (a x h)/ 2
=> Trong đó
- a: Chiều dài đáy tam giác đều (đáy là một trong 3 cạnh của tam giác)
- h: Chiều cao của tam giác (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy).
– Mong rằng những chia sẽ trên sẽ giúp cho bạn một phần nào đó trong việc học tập của mình. Xin chân thành cảm ơn bạn khi đã xem hết bài viết này. Để có thể xem thêm nhiều bài viết hơn nữa hãy truy cập vào trang: bluefone.com.vn